Question

阅读下列材料，然后解答后面的问题．

我们知道方程2x+3y=12有无数组解，但在实际生活中我们往往只需要求出其正整数解．

例：由2x+3y=12，得，（x、y为正整数）

∴，解得0＜x＜6．

又为正整数，则为正整数．

由2与3互质，可知：x为3的倍数，从而x=3，代入．

∴2x+3y=12的正整数解为

问题：

（1）请你写出方程2x+y=5的一组正整数解：　　；

（2）若为自然数，则满足条件的x值有　　个；

A．2                B．3                C．4                D．5

（3）七年级某班为了奖励学习进步的学生，购买了单价为3元的笔记本与单价为5元的钢笔两种奖品，共花费35元，问有几种购买方案？

 

Answer 1

【答案】

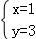（1）或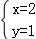；（2）C；（3）两种

【解析】

试题分析：根据题意可知，求方程的正整数解，先把方程做适当的变形，再列举正整数代入求解．

（1） 由2x+y=5，得y=5-2x（x、y为正整数）

所以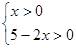，解得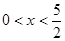

∴当x=1时，y=3；

当x=2时，y=1．

即方程的正整数解是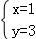或；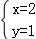

（2）同样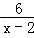为自然数，则有：0＜x-2≤6，即2＜x≤8

当x=3时，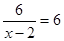

当x=4时，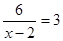

当x=5时，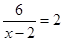

当x=8时，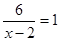

即满足条件x的值有4个，

故选C；

（3）设购买单价为3元的笔记本m本，单价为5元的钢笔n支．

则根据题意得：3m+5n=35，其中m、n均为自然数，则

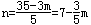
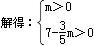
所以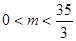

由于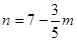为正整数，则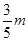为正整数，可知m为5的倍数．

∴当m=5时，n=4；

当m=10时，n=1．

答：有两种购买方案：即购买单价为3元的笔记本5本，单价为5元的钢笔4支；

或购买单价为3元的笔记本10本，单价为5元的钢笔1支．

考点：二元一次方程组的应用

点评：解题关键是要读懂题目给出的已知条件，根据条件求解．注意笔记本和钢笔是整体，所有不可能出现小数和负数，这也就说要求的是正整数．