题目内容
9.Rt△ABC中,∠C=90°,点D是AB边的中点,则$\frac{CD}{AB}$=$\frac{1}{2}$.分析 根据直角三角形斜边上的中线等于斜边的一半即可解答.
解答  解:如图.
解:如图.
∵Rt△ABC中,∠ACB=90°,点D是AB的中点,
∴CD=$\frac{1}{2}$AB,
∴$\frac{CD}{AB}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查的是直角三角形的性质,掌握直角三角形斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.两条直线相交可以形成2对对顶角,那么同一平面内4条直线最多可以形成对顶角( )
| A. | 8对 | B. | 10对 | C. | 12对 | D. | 16对 |
20.泗阳华润苏果超市准备购进A、B两种品牌的书包共100个,已知两种书包的进价如下表所示,设购进A种书包x个,且所购进的两种书包能全部卖出,获得的总利润为y元.
(1)将表格的信息填写完整;
(2)求y关于x的函数表达式;
(3)如果购进两种书包的总费用不超过4500元且购进B种书包的数量不大于A种书包的3倍,那么超市如何进货才能获利最大?并求出最大利润.
| 品牌 | 购买个数(个) | 进价(元/个) | 售价(元/个) | 获利(元) |
| A | x | 50 | 60 | 10x |
| B | 100-x | 40 | 55 | 15(100-x) |
(2)求y关于x的函数表达式;
(3)如果购进两种书包的总费用不超过4500元且购进B种书包的数量不大于A种书包的3倍,那么超市如何进货才能获利最大?并求出最大利润.
1.服装店销售某款服装,每件服装的标价为300元,若按标价的八折销售,仍可获利60元,则这款服装每件的标价比进价多( )
| A. | 60元 | B. | 80元 | C. | 120元 | D. | 180元 |
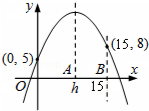 已知二次函数y=a(x-h)2+k(a,h,k为常数)在坐标平面上的图象通过(0,5)、(15,8)两点.若a<0,0<h<10,则h之值可能为下列何值?( )
已知二次函数y=a(x-h)2+k(a,h,k为常数)在坐标平面上的图象通过(0,5)、(15,8)两点.若a<0,0<h<10,则h之值可能为下列何值?( )