题目内容
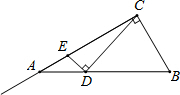 如图在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=2,D是AB边上的一个动点(不与点A、B重合),过点D作CD的垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示y与x的函数关系图象大致是( )
如图在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=2,D是AB边上的一个动点(不与点A、B重合),过点D作CD的垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示y与x的函数关系图象大致是( )A、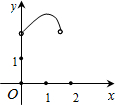 | B、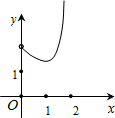 | C、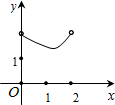 | D、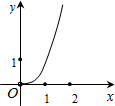 |
分析:本题需先根据题意,求出BC、AC的长,再分别计算出当x=0和x=2时,y的值,即可得出y与x的函数关系图象.
解答:解:∵∠ACB=90°,∠BAC=30°,AB=2,
∴BC=1,AC=
,
∴当x=0时,y的值是
,
当x=1时,y的值是
,
∵当x=2时CD的垂线与CA平行,虽然x不能取到2,但y应该是无穷大,
∴y与x的函数关系图象大致是B,
过点D作点DG⊥AC于点G,过点D作点DF⊥BC于点F,
∴CF=DG=
,DF=CG=
(2-x),
∴EG=y-CG,
分别在直角三角形CDF、直角三角形DGE、直角三角形CDE中利用勾股定理,
DF2+CF2+DG2+GE2=CE2,
y=
,
故选B.
∴BC=1,AC=
| 3 |
∴当x=0时,y的值是
| 3 |
当x=1时,y的值是
2
| ||
| 3 |
∵当x=2时CD的垂线与CA平行,虽然x不能取到2,但y应该是无穷大,
∴y与x的函数关系图象大致是B,
过点D作点DG⊥AC于点G,过点D作点DF⊥BC于点F,

∴CF=DG=
| x |
| 2 |
| ||
| 2 |
∴EG=y-CG,
分别在直角三角形CDF、直角三角形DGE、直角三角形CDE中利用勾股定理,
DF2+CF2+DG2+GE2=CE2,
y=
| 2x2-6x+6 | ||
|
故选B.
点评:本题主要考查了动点问题的函数图象,在解题时要能根据题意得出函数关系本题的关键.

练习册系列答案
相关题目
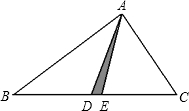 如图在Rt△ABC中,∠BAC=90°,AB=5,AC=4,AD、AE分别是△ABC的中线和角平分线,则△ADE的面积为
如图在Rt△ABC中,∠BAC=90°,AB=5,AC=4,AD、AE分别是△ABC的中线和角平分线,则△ADE的面积为 如图在Rt△ABC中,∠ACB=90°,sinA=
如图在Rt△ABC中,∠ACB=90°,sinA=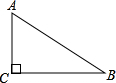 如图在Rt△ABC中,∠C=90°,AC=5,AB=13,则tanB=
如图在Rt△ABC中,∠C=90°,AC=5,AB=13,则tanB=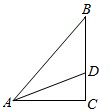 如图在Rt△ABC中,AD平分∠CAB,CD=8cm,那么点D到AB的距离是
如图在Rt△ABC中,AD平分∠CAB,CD=8cm,那么点D到AB的距离是 (1)如图在Rt△ABC中,CD是AB边上的高,若AD=8,BD=2,则CD=
(1)如图在Rt△ABC中,CD是AB边上的高,若AD=8,BD=2,则CD=