Question

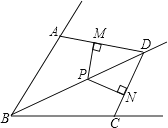
【题目】如图，在菱形ABCD中，AC交BD于P，E为BC上一点，AE交BD于F，若AB=AE，，则下列结论：①AF=AP；②AE=FD；③BE=AF．正确的是______（填序号）．

Answer 1

【答案】②③

【解析】

根据菱形的性质可知AC⊥BD，所以在Rt△AFP中，AF一定大于AP，从而判断①；设∠BAE=x，然后根据等腰三角形两底角相等表示出∠ABE，再根据菱形的邻角互补求出∠ABE，根据三角形内角和定理列出方程，求出x的值，求出∠BFE和∠BE的度数，从而判断②③．

解：在菱形ABCD中，AC⊥BD，

∴在Rt△AFP中，AF一定大于AP，故①错误；

∵四边形ABCD是菱形，

∴AD∥BC，

∴∠ABE+∠BAE+∠EAD=180°，

设∠BAE=x°，

则∠EAD=2x°，∠ABE=180°-x°-2x°，

∵AB=AE，∠BAE=x°，

∴∠ABE=∠AEB=180°-x°-2x°，

由三角形内角和定理得：x+180-x-2x+180-x-2x=180，

解得：x=36，

即∠BAE=36°，

∠BAE=180°-36°-2×36°=70°，

∵四边形ABCD是菱形，

∴∠BAD=∠CBD=∠ABE=36°，

∴∠BFE=∠ABD+∠BAE=36°+36°=72°，

∴∠BEF=180°-36°-72°=72°，

∴BE=BF=AF．故③正确

∵∠AFD=∠BFE=72°，∠EAD=2x°=72°

∴∠AFD=∠EAD

∴AD=FD

又∵AD=AB=AE

∴AE=FD，故②正确

∴正确的有②③

故答案为：②③