题目内容
17.某现代农业示范园区准备租用甲、乙两种货车将一批蔬菜运到城区销售,已知一辆甲种货车可装茄子4吨和玉米1吨,一辆乙种货车可装茄子和玉米各2吨,若园区要求安排甲,乙两种货车共10辆一次性运输茄子和玉米,其中茄子不少于30吨,玉米不少于13吨.(1)那么园区如何安排甲,乙两种货车进行运输?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费280元,则园区应选择哪种方案,使运输费最少?最少运费是多少?
分析 (1)本题可设安排甲种货车x辆,则安排乙种货车(10-x)辆,然后根据题意列出不等式组:$\left\{\begin{array}{l}{4x+2(10-x)≥30}\\{x+2(10-x)≥13}\end{array}\right.$,化简后得出x的取值范围,看其中有几个整数即可得知有几种方案.
(2)本题可根据第一题列出的几种方案得出方案一所需的运费少,依此即可得出答案.
解答 解:(1)设安排甲种货车x辆,则安排乙种货车(10-x)辆,依题意得
$\left\{\begin{array}{l}{4x+2(10-x)≥30}\\{x+2(10-x)≥13}\end{array}\right.$,
解此不等式组得5≤x≤7.
∵x是正整数
∴x可取的值为5,6,7.
∴安排甲、乙两种货车有三种方案:
| 甲种货车 | 乙种货车 | |
| 方案一 | 5辆 | 5辆 |
| 方案二 | 6辆 | 4辆 |
| 方案三 | 7辆 | 3辆 |
∴选择方案一运费最少,最少运费是300×5+280×5=2900(元).
答:园区应选择方案一,使运输费最少,最少运费是2900元.
点评 本题考查的是一元一次不等式组的运用,解此类题目要注意根据题意列出不同的式子比较值大小.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
8.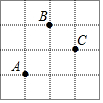 在如图的方格纸上,若用(-1,1)表示A点,(0,3)表示B点,那么C点的位置可表示为( )
在如图的方格纸上,若用(-1,1)表示A点,(0,3)表示B点,那么C点的位置可表示为( )
 在如图的方格纸上,若用(-1,1)表示A点,(0,3)表示B点,那么C点的位置可表示为( )
在如图的方格纸上,若用(-1,1)表示A点,(0,3)表示B点,那么C点的位置可表示为( )| A. | (1,2) | B. | (2,3) | C. | (3,2) | D. | (2,1) |
5. 如图,菱形ABCD的周长为32cm,对角线AC、BD相交于点O,E是AD的中点,连接OE,则线段OE的长等于( )
如图,菱形ABCD的周长为32cm,对角线AC、BD相交于点O,E是AD的中点,连接OE,则线段OE的长等于( )
 如图,菱形ABCD的周长为32cm,对角线AC、BD相交于点O,E是AD的中点,连接OE,则线段OE的长等于( )
如图,菱形ABCD的周长为32cm,对角线AC、BD相交于点O,E是AD的中点,连接OE,则线段OE的长等于( )| A. | 3cm | B. | 3.5cm | C. | 4cm | D. | 5cm |
12. 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,2),第2次接着运动到点(4,0),第3次接着运动到点(6,1),…,按这样的运动规律,经过第72次运动后,动点P的坐标是( )
如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,2),第2次接着运动到点(4,0),第3次接着运动到点(6,1),…,按这样的运动规律,经过第72次运动后,动点P的坐标是( )
 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,2),第2次接着运动到点(4,0),第3次接着运动到点(6,1),…,按这样的运动规律,经过第72次运动后,动点P的坐标是( )
如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,2),第2次接着运动到点(4,0),第3次接着运动到点(6,1),…,按这样的运动规律,经过第72次运动后,动点P的坐标是( )| A. | (144,0) | B. | (142,2) | C. | (72,0) | D. | (142,1) |
6.下列事件中,是必然事件的为( )
| A. | 明天会下雨 | B. | x是实数,x2<0 | ||
| C. | 两个奇数之和为偶数 | D. | 异号两数相加,和为负数 |
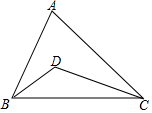 如图,在△ABC中,∠A=70°,D是△ABC内一点,若∠ABD=30°,∠ACD=25°,则∠BDC=125°.
如图,在△ABC中,∠A=70°,D是△ABC内一点,若∠ABD=30°,∠ACD=25°,则∠BDC=125°.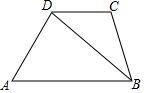 如图,已知四边形ABCD中,∠BCD=100°,BD平分∠ABC,且∠ABD=40°.
如图,已知四边形ABCD中,∠BCD=100°,BD平分∠ABC,且∠ABD=40°.