题目内容
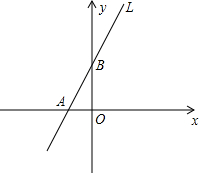（2013•花都区一模）如图，已知直线L：y=2x+2与x轴、y轴分别相交于A、B两点（1）求点A、B的坐标；
（2）把直线L绕点B顺时针旋转90°得直线L′，作出直线L′，并在直线L′标出点A的对应点A′的位置；
（3）求由直线L、L′和x轴所围成三角形的周长．
分析：（1）根据直线L的解析式，可求出点A、B的坐标；
（2）根据题意作出图形即可；
（3）先求出AB的长度，判断△ABC∽△AOB，利用相似三角形的性质可求出AC，在Rt△ABC中求出BC，从而可求出△ABC的周长．
（2）根据题意作出图形即可；
（3）先求出AB的长度，判断△ABC∽△AOB，利用相似三角形的性质可求出AC，在Rt△ABC中求出BC，从而可求出△ABC的周长．
解答：解：（1）当y=0时，2x+2=0，
解得：x=-1
则点A的坐标为（-1，0），
当x=0时，y=2，
则点B的坐标为（0，2）．
（2）如图所示，直线L'和点A'为所求
．
（3）设直线L'与x轴相交于点C，
在Rt△ABO中，AB=
=
=
，
∵∠ABC=∠AOB=90°，∠A=∠A，
∴△ABC∽△AOB，
∴
=
，
∴
=
，
解得：AC=5，
在Rt△ABC中，BC=
=
=2
，
故△ABC的周长=AB+BC+AC=
+2
+5=3
+5．
解得：x=-1
则点A的坐标为（-1，0），
当x=0时，y=2，
则点B的坐标为（0，2）．
（2）如图所示，直线L'和点A'为所求
．（3）设直线L'与x轴相交于点C，
在Rt△ABO中，AB=
| AO2+BO2 |
| 12+22 |
| 5 |
∵∠ABC=∠AOB=90°，∠A=∠A，
∴△ABC∽△AOB，
∴
| AB |
| AC |
| AO |
| AB |
∴
| ||
| AC |
| 1 | ||
|
解得：AC=5，
在Rt△ABC中，BC=
| AC2+AB2 |
52-(
|
| 5 |
故△ABC的周长=AB+BC+AC=
| 5 |
| 5 |
| 5 |
点评：本题考查了一次函数综合题，涉及了图形的旋转、相似三角形的判定与性质，难点在第三问，关键是根据相似三角形的对应边成比例求出AC，有一定难度．
练习册系列答案
相关题目
（2013•花都区一模）已知：四边形ABCD是平行四边形，点E是BC上的一点，且∠DAE=∠B