题目内容
已知|a+1|与(2-b)2互为相反数,求(a+b)2013+a2014的值.
考点:非负数的性质:偶次方,非负数的性质:绝对值
专题:
分析:根据互为相反数的两个数的和等于0列出方程,再根据非负数的性质列式求出a、b,然后代入代数式进行计算即可得解.
解答:解:∵|a+1|与(2-b)2互为相反数,
∴|a+1|+(2-b)2=0,
∴a+1=0,2-b=0,
解得a=-1,b=2,
所以,(a+b)2013+a2014=(-1+2)2013+(-1)2014=1+1=2.
∴|a+1|+(2-b)2=0,
∴a+1=0,2-b=0,
解得a=-1,b=2,
所以,(a+b)2013+a2014=(-1+2)2013+(-1)2014=1+1=2.
点评:本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
相关题目
若不等式4x+1<a的正整数解是1、2,则实数a不可以取的值是( )
| A、13 | B、11 | C、9.6 | D、9 |
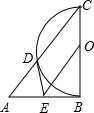 如图,以Rt△ABC的直角边BC为直径作半圆O交斜边于D,OE∥AC,交AB于E,连接DE.
如图,以Rt△ABC的直角边BC为直径作半圆O交斜边于D,OE∥AC,交AB于E,连接DE.