题目内容
已知正三角形ABC,AB=a,点P,Q分别从A,C两点同时出发,以相同速度作直线运动,且点P沿射线AB方向运动,点Q沿射线BC方向运动.设AP的长为x,△PCQ的面积为S,
(1)求S关于x的函数关系式;
(2)当AP的长为多少时,△PCQ的面积和△ABC的面积相等?
(1)求S关于x的函数关系式;
(2)当AP的长为多少时,△PCQ的面积和△ABC的面积相等?
分析:(1)分当0<x<a时和当x>a时,作PM⊥BQ,表示出线段PM=
(a-x),利用三角形的面积公式写出S与x的函数关系式即可;
(2)首先表示出S△ABC,分0<x<a时和当x>a时列出方程求解x的值即可.
| ||
| 2 |
(2)首先表示出S△ABC,分0<x<a时和当x>a时列出方程求解x的值即可.
解答: 解:(1)当0<x<a时,作PM⊥BQ(如图1),
解:(1)当0<x<a时,作PM⊥BQ(如图1),
则PM=
(a-x),CQ=AP=x,所以S=
×CQ•PM=
x(a-x).
当x=a时,S=0.
当x>a时,同样作PM⊥BQ(如图2),
 则PM=
则PM=
(x-a),所以S=
×CQ•PM=
x(x-a).
(2)S△ABC=
a2.
当0<x<a时,由
x(a-x)=
a2,
得x2-ax+a2=0.
因为b2-4ac=-3a2<0,
所以此方程无解.
当x>a时,由
x(x-a)=
a2,
得x2-ax-a2=0.
解得x=
.x=
不合题意舍去,
所以x=
,
即当x=
时,△PCQ的面积和△ABC的面积相等.
 解:(1)当0<x<a时,作PM⊥BQ(如图1),
解:(1)当0<x<a时,作PM⊥BQ(如图1),则PM=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
当x=a时,S=0.
当x>a时,同样作PM⊥BQ(如图2),
 则PM=
则PM=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
(2)S△ABC=
| ||
| 4 |
当0<x<a时,由
| ||
| 4 |
| ||
| 4 |
得x2-ax+a2=0.
因为b2-4ac=-3a2<0,
所以此方程无解.
当x>a时,由
| ||
| 4 |
| ||
| 4 |
得x2-ax-a2=0.
解得x=
a±
| ||
| 2 |
a-
| ||
| 2 |
所以x=
a+
| ||
| 2 |
即当x=
a+
| ||
| 2 |
点评:本题考查了二次函数的综合知识,根据题意分类讨论列出函数的关系式是解决本题的关键.

练习册系列答案
相关题目

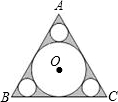 如图,已知正三角形ABC的边长为6,在△ABC中作内切圆O及三个角切圆(我们把与角两边及三角形内切圆都相切的圆叫角切圆),则△ABC的内切圆O的面积为
如图,已知正三角形ABC的边长为6,在△ABC中作内切圆O及三个角切圆(我们把与角两边及三角形内切圆都相切的圆叫角切圆),则△ABC的内切圆O的面积为 点A运动.
点A运动.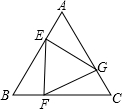 如图,已知正三角形ABC的边长为1,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数的图象大致是( )
如图,已知正三角形ABC的边长为1,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数的图象大致是( )