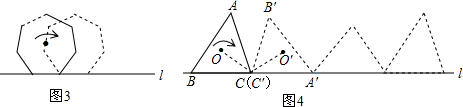
题目内容
已知正三角形ABC的边长为1，按如图所示位置放在直线m上，然后无滑动地滚动，当它滚动一个周期时，顶点A所经过的路线长为多少？
分析：根据正三角形的性质及弧长公式求出点A绕点B、点C旋转的两段弧长相加即可．
解答：解：∵点A所经过的这两段弧所在圆的半径为1，所对圆心角均为120度
∴点A所经过的路线长为2×
=
π（8分）
∴点A所经过的路线长为2×
| 120π×1 |
| 180 |
| 4 |
| 3 |
点评：本题主要考查了正三角形的性质及弧长公式l=
πr．
| n |
| 180 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
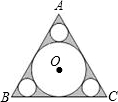如图，已知正三角形ABC的边长为6，在△ABC中作内切圆O及三个角切圆（我们把与角两边及三角形内切圆都相切的圆叫角切圆），则△ABC的内切圆O的面积为
点A运动．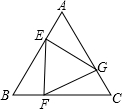
如图，已知正三角形ABC的边长为1，E，F，G分别是AB，BC，CA上的点，且AE=BF=CG，设△EFG的面积为y，AE的长为x，则y关于x的函数的图象大致是（ ）
