题目内容
解下列方程:
(1)9t2-(t-1)2=0;
(2)2x2-5x+1=0(配方法).
(1)9t2-(t-1)2=0;
(2)2x2-5x+1=0(配方法).
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:计算题
分析:(1)方程左边利用平方差公式分解后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解;
(2)方程二次项系数化为1,常数项移到右边,两边加上一次项系数一半的平方,利用完全平方公式变形后,开方即可求出解.
(2)方程二次项系数化为1,常数项移到右边,两边加上一次项系数一半的平方,利用完全平方公式变形后,开方即可求出解.
解答:解:(1)方程分解因式得:(3t+t-1)(3t-t+1)=0,
可得4t-1=0或2t+1=0,
解得:t1=-
,t2=
;
(2)方程变形得:x2-
x=-
,
配方得:x2-
x+
=
,即(x-
)2=
,
开方得:x=
±
.
可得4t-1=0或2t+1=0,
解得:t1=-
| 1 |
| 2 |
| 1 |
| 4 |
(2)方程变形得:x2-
| 5 |
| 2 |
| 1 |
| 2 |
配方得:x2-
| 5 |
| 2 |
| 25 |
| 16 |
| 17 |
| 16 |
| 5 |
| 4 |
| 17 |
| 16 |
开方得:x=
| 5 |
| 4 |
| ||
| 4 |
点评:此题考查了解一元二次方程-因式分解法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
已知a>0,且(2-b)a<0,则b的值可以是( )
| A、-1 | ||
| B、0 | ||
C、
| ||
D、2
|
若方程x2-4x+c=0有两个相等的实数根,则实数c的值是( )
| A、6 | B、5 | C、4 | D、3 |
 建立直角坐标系,标出以下各组点,并将各组内的点用线段依次连接起来,观察所得的图形,你认为它是什么?
建立直角坐标系,标出以下各组点,并将各组内的点用线段依次连接起来,观察所得的图形,你认为它是什么?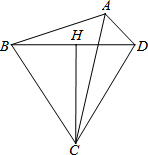 已知:四边形ABCD中,∠ABC+∠ADC=180°,CH垂直平分BD
已知:四边形ABCD中,∠ABC+∠ADC=180°,CH垂直平分BD