题目内容
 已知平面直角坐标系xOy(如图),一次函数y=
已知平面直角坐标系xOy(如图),一次函数y=| 3 |
| 4 |
| 3 |
| 2 |
(1)求线段AM的长;
(2)求这个二次函数的解析式;
(3)如果点B在y轴上,且位于点A下方,点C在上述二次函数的图象上,点D在一次函数y=
| 3 |
| 4 |
分析:(1)先求出根据OA垂直平分线上的解析式,再根据两点的距离公式求出线段AM的长;
(2)二次函数y=x2+bx+c的图象经过点A、M.待定系数法即可求出二次函数的解析式;
(3)可设D(n,
n+3),根据菱形的性质得出C(n,n2_
n+3)且点C在二次函数y=x2_
x+3上,得到方程求解即可.
(2)二次函数y=x2+bx+c的图象经过点A、M.待定系数法即可求出二次函数的解析式;
(3)可设D(n,
| 3 |
| 4 |
| 5 |
| 2 |
| 5 |
| 2 |
解答: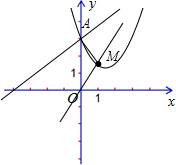 解:(1)在一次函数y=
解:(1)在一次函数y=
x+3中,
当x=0时,y=3.
∴A(0,3).
∵MO=MA,
∴M为OA垂直平分线上的点,
可求OA垂直平分线上的解析式为y=
x,
又∵点M在正比例函数y=
x,
∴M(1,
),
又∵A(0,3).
∴AM=
;
(2)∵二次函数y=x2+bx+c的图象经过点A、M.可得
,
解得
.
∴y=x2-
x+3;
(3)∵点D在一次函数y=
x+3的图象上,
则可设D(n,
n+3),
设B(0,m),(m<3),C(n,n2-
n+3)
∵四边形ABDC是菱形,
∴|AB|=3-m,|DC|=|yD-yC|=|
n+3-(n2_
n+3)|=|
n-n2|,
|AD|=
=|
n|,
∵|AB|=|DC|,
∴3-m=
n-n2,①,
∵|AB|=|DA|,
∴3-m=
n,②
解①②得,n1=0(舍去),n2=2,
将n=2,代入C(n,n2_
n+3),
∴C(2,2).
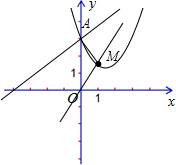 解:(1)在一次函数y=
解:(1)在一次函数y=| 3 |
| 4 |
当x=0时,y=3.
∴A(0,3).
∵MO=MA,
∴M为OA垂直平分线上的点,
可求OA垂直平分线上的解析式为y=
| 3 |
| 2 |
又∵点M在正比例函数y=
| 3 |
| 2 |
∴M(1,
| 3 |
| 2 |
又∵A(0,3).
∴AM=
| ||
| 2 |
(2)∵二次函数y=x2+bx+c的图象经过点A、M.可得
|
解得
|
∴y=x2-
| 5 |
| 2 |
(3)∵点D在一次函数y=
| 3 |
| 4 |
则可设D(n,
| 3 |
| 4 |
设B(0,m),(m<3),C(n,n2-
| 5 |
| 2 |
∵四边形ABDC是菱形,
∴|AB|=3-m,|DC|=|yD-yC|=|
| 3 |
| 4 |
| 5 |
| 2 |
| 13 |
| 4 |
|AD|=
(n-0) 2+(
|
| 5 |
| 4 |
∵|AB|=|DC|,
∴3-m=
| 13 |
| 4 |
∵|AB|=|DA|,
∴3-m=
| 5 |
| 4 |
解①②得,n1=0(舍去),n2=2,
将n=2,代入C(n,n2_
| 5 |
| 2 |
∴C(2,2).
点评:本题是二次函数的综合题型,其中涉及的知识点有抛物线解析式的确定,两点的距离公式,菱形的性质,解二元一次方程,综合性较强,难度较大.

练习册系列答案
相关题目

 如图,已知平面直角坐标系,A、B两点的坐标分别为A(2,-3),B(4,-1).若C(a,0),D(a+3,0)是x轴上的两个动点,则当a=
如图,已知平面直角坐标系,A、B两点的坐标分别为A(2,-3),B(4,-1).若C(a,0),D(a+3,0)是x轴上的两个动点,则当a= (2013•上海)已知平面直角坐标系xOy(如图),直线
(2013•上海)已知平面直角坐标系xOy(如图),直线