题目内容
5.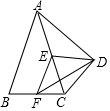 如图,在四边形ABCD中,∠ADC=90°,AB=AC,E,F分别为AC,BC的中点,连接EF,ED,FD.
如图,在四边形ABCD中,∠ADC=90°,AB=AC,E,F分别为AC,BC的中点,连接EF,ED,FD.(1)求证:ED=EF;
(2)若∠BAD=60°,AC平分∠BAD,AC=6,求DF的长.
分析 (1)由直角三角形的性质可知DE=$\frac{1}{2}$AC,由三角形中位线定理可得EF=$\frac{1}{2}$AB,由条件AB=AC,可证得结论;
(2)由条件可证得△DEF为等腰直角三角形,利用勾股定理可求得DF的长.
解答 (1)证明:
∵∠ADC=90°,E为AC的中点,
∴DE=AE=$\frac{1}{2}$AC,
∵F为BC的中点,
∴EF为△ABC的中位线,
∴EF=$\frac{1}{2}$AB,
∵AB=AC,
∴DE=EF;
(2)解:
∵∠BAD=60°,AC平分∠BAD,
∴∠BAC=∠DAC=$\frac{1}{2}$∠BAD=30°,
由(1)可知EF∥AB,AE=DE,
∴∠FEC=∠BAC=30°,∠DEA=2∠DAC=60°,
∴∠FED=90°,
∵AC=6,
∴DE=EF=3,
∴DF=$\sqrt{D{E}^{2}+E{F}^{2}}$=3$\sqrt{2}$.
点评 本题主要考查三角形中位线定理及直角三角形的性质,利用条件分别得到DE为直角三角形斜边上的中线、EF为三角形的中位线是解题的关键.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
16.若代数式3x-4与-2x+1的值相等,则x的值是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
17.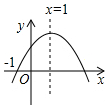 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
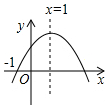 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )| A. | a>0 | B. | 当x>1时,y随x的增大而增大 | ||
| C. | c<0 | D. | 3是方程ax2+bx+c=0的一个根 |

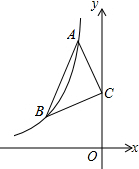 如图,△ABC的顶点A,B都在反比例函数y=-$\frac{6}{x}$的第二象限内的分支上,点C(0,3),且AC=BC,∠ACB=90°,则线段AB的长为2$\sqrt{5}$.
如图,△ABC的顶点A,B都在反比例函数y=-$\frac{6}{x}$的第二象限内的分支上,点C(0,3),且AC=BC,∠ACB=90°,则线段AB的长为2$\sqrt{5}$.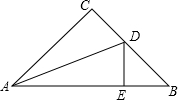 如图,在△ABC中,∠C=90°,AC=BC=a,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=8,则△DEB的周长为( )
如图,在△ABC中,∠C=90°,AC=BC=a,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=8,则△DEB的周长为( )