题目内容
若有理数x，y满足|2x-1|+y2-4y=-4，则x•y的值等于
- A.-1
- B.1
- C.-2
- D.2
B
分析：先移项，再由非负数的性质，列方程求得x、y的值，代入即可．
解答：∵|2x-1|+y2-4y=-4，
∴|2x-1|+y2-4y+4=0，即|2x-1|+（y-2）2=0，
∴
，解得x=
，y=2，
∴xy=
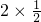=1，
故选B．
点评：本题主要考查非负数的性质和完全平方公式的变形，熟记公式结构是解题的关键．完全平方公式：（a±b）2=a2±2ab+b2．
分析：先移项，再由非负数的性质，列方程求得x、y的值，代入即可．
解答：∵|2x-1|+y2-4y=-4，
∴|2x-1|+y2-4y+4=0，即|2x-1|+（y-2）2=0，
∴
，解得x=，y=2，∴xy=
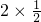=1，故选B．
点评：本题主要考查非负数的性质和完全平方公式的变形，熟记公式结构是解题的关键．完全平方公式：（a±b）2=a2±2ab+b2．
练习册系列答案
相关题目