题目内容
请观察下列算式,找出规律并填空| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
则第10个算式是
第n个算式为
根据以上规律解答下题:
若有理数a,b满足|a-1|+(b-3)2=0,试求:
| 1 |
| ab |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+4)(b+4) |
| 1 |
| (a+100)(b+100) |
分析:根据所给的算式,可找出规律:
=
-
;现根据所给的式子,利用两个非负数的和等于,则每一个非负数等于0,可求出a、b,再把a、b的值代入所求式子,利用公式
=
×(
-
)进行计算即可.
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
解答:解:
;
-
;
;
-
.
∵|a-1|+(b-3)2=0,
∴a=1,b=3,
∴
+
+
+…+
,
=
+
+
+…+
,
=
×(1-
+
-
+…+
-
),
=
×(1-
),
=
×
,
=
.
| 1 |
| 10×11 |
| 1 |
| 10 |
| 1 |
| 11 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∵|a-1|+(b-3)2=0,
∴a=1,b=3,
∴
| 1 |
| ab |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+4)(b+4) |
| 1 |
| (a+100)(b+100) |
=
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 101×103 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 101 |
| 1 |
| 103 |
=
| 1 |
| 2 |
| 1 |
| 103 |
=
| 1 |
| 2 |
| 102 |
| 103 |
=
| 51 |
| 103 |
点评:本题主要是寻找规律,再根据有理数的混合运算计算,并利用了两个非负数的和等于0,则每一个非负数等于0的知识.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 =1-
=1- ,
, =
= ,
, =
= ,
,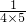 =
=
 +
+ +
+ +…+
+…+ 的值.
的值.