Question

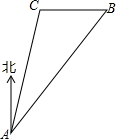如图，在小岛上有一观测站A，灯塔B在观测站A北偏东45°的方向．灯塔C在灯塔B的正西方向，且相距10海里，灯塔C与观测站A相距10

2

海里，请你测算灯塔C处在观测站A的什么方向？

Answer 1

考点：解直角三角形的应用-方向角问题

专题：

分析：过点C作CD⊥AB，垂足为D，设AD=x，根据锐角三角函数的定义求出CD、AC的长度，再根据∠CAF=∠BAF-∠CAD即可判断出点C的位置．

解答：解：过点C作CD⊥AB，垂足为D．
∵灯塔B在观察站A北偏东45°的方向，
∴∠B=45°．
又∵BC=10海里
∴在Rt△BCD中，sin∠B=

CD

BC

，
∴sin45°=

CD

BC

，
∴CD=BC•sin45°=10×

2

2

=5

2

（海里）．
在Rt△ACD中，
∵AC=10

2

，
∴sin∠CAD=

CD

AC

=

5 2

10 2

=

1

2

，即sin∠CAD=

1

2

，
∴∠CAD=30°
∴∠CAF=∠BAF-∠CAD=45°-30°=15°
答：灯塔C处在观察站A北偏东15°的方向．

点评：本题考查解直角三角形的应用-方向角问题，解答此题的关键在于根据题意画出示意图，然后根据已知线段利用三角函数的关系进行解答．