题目内容
有一种传染性疾病,蔓延速度极快,通常情况下,每人一天能传染给若干人,现有五人患了这种疾病,两天后有245人患了这种病,求平均每天每人传染了几个人?
考点:一元二次方程的应用
专题:
分析:根据第一天患病的人数为5+5×传播的人数,第二天患病的人数为第一天患病的人数×传播的人数,再根据等量关系:第一天患病的人数+第二天患病的人数=245,列出方程求解即可.
解答:解:设平均每天每人传染了x个人,根据题意得:
5+5x+(5+5x)×x=245,
(1+x)2=49,
解得:1+x=±7,
x1=6,x2=-8(舍去).
答:平均每天每人传染了6个人.
5+5x+(5+5x)×x=245,
(1+x)2=49,
解得:1+x=±7,
x1=6,x2=-8(舍去).
答:平均每天每人传染了6个人.
点评:此题考查了一元二次方程的应用,读懂题意,得到两天患病人数的等量关系是解决本题的关键;本题的等量关系是:第一天患病的人数+第二天患病的人数=245.

练习册系列答案
相关题目
满足下列条件的△ABC,不是直角三角形的是( )
| A、b2=c2-a2 |
| B、a:b:c=3:4:6 |
| C、∠C=∠A+∠B |
| D、∠A:∠B:∠C=9:16:25 |
 如图,AB=AC,AD=AE,求证:DE⊥BC.
如图,AB=AC,AD=AE,求证:DE⊥BC. 如图所示图形,用代数式表示该图形的面积,并计算当x=10,y=14时,图形的面积.
如图所示图形,用代数式表示该图形的面积,并计算当x=10,y=14时,图形的面积.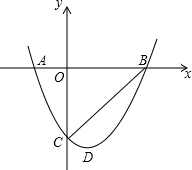 如图,已知抛物线y=x2-2x-3与x轴从左至右分别交于A、B两点,与y轴交于C点,顶点为D.
如图,已知抛物线y=x2-2x-3与x轴从左至右分别交于A、B两点,与y轴交于C点,顶点为D.