题目内容
8.(1)如图1,请直接写出∠A+∠B+∠C+∠D+∠E的结果;(2)将图1变形为图2,∠A+∠DBE+∠C+∠D+∠E的结果如何?请写出证明过程;
(3)将图1变形为图3,则∠A+∠B+∠C+∠D+∠E的结果如何?请写出证明过程.
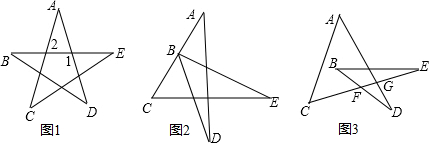
分析 (1)根据三角形外角的性质∠2=∠C+∠E,∠1=∠A+∠2,根据三角形内角和等于180°即可求解.
(2)根据三角形外角的性质∠ABE=∠C+∠E,∠DBC=∠A+∠D,即可证明此结论.
(3)根据三角形外角的性质,∠DFG=∠B+∠E,∠FGD=∠A+∠C,即可证明此结论.
解答 (1)解:∵∠2=∠C+∠E,∠1=∠A+∠2,
∴∠A+∠B+∠C+∠D+∠E=∠1+∠B+∠D=180°;
(2)证明:∵∠ABE=∠C+∠E,∠DBC=∠A+∠D,
∠ABE+∠DBE+∠DBC=180°,
∴∠A+∠DBE+∠C+∠D+∠E=180°
∴将图①变形成图②∠A+∠DBE+∠C+∠D+∠E仍然为180°;
(3)证明:∵在△FGD中,∠DFG+∠FGD+∠D=180°,
∠DFG=∠B+∠E,∠FGD=∠A+∠C,
∴∠A+∠B+∠C+∠D+∠E=180°,
∴将图①变形成图③,则∠A+∠B+∠C+∠D+∠E还为180°.
点评 此题主要考查三角形内角和定理和三角形外角的性质,难度不大,属于基础题.

练习册系列答案
相关题目
 如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).点E(2,m)在抛物线上,抛物线的对称轴与x轴交于点H,点F是AE中点,连接FH,求线段FH的长.
如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).点E(2,m)在抛物线上,抛物线的对称轴与x轴交于点H,点F是AE中点,连接FH,求线段FH的长.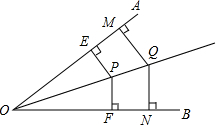 如图,P是∠AOB内部的一点,PE⊥OA,PF⊥OB垂足分别为E,F.PE=PF.Q是OP上的任意一点,QM⊥OA,QN⊥OB,垂足分别为点M和N,QM与QN相等吗?请证明.
如图,P是∠AOB内部的一点,PE⊥OA,PF⊥OB垂足分别为E,F.PE=PF.Q是OP上的任意一点,QM⊥OA,QN⊥OB,垂足分别为点M和N,QM与QN相等吗?请证明.