题目内容
1．
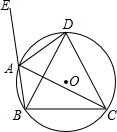如图．已知四边形ABCD内接于⊙O，DB=DC，延长BA至点E，求证：AD是△ABC的外角∠EAC的角平分线．
分析 根据圆内接四边形的性质得到∠DCB=∠EAD，根据等腰三角形的性质得到∠DCB=∠DBC，根据圆周角定理得到∠DBC=∠DAC，等量代换得到答案．
解答 证明：∵四边形ABCD内接于⊙O，
∴∠DCB=∠EAD，
∵DB=DC，
∴∠DCB=∠DBC，又∠DBC=∠DAC，
∴∠DCB=∠DAC，
∴∠EAD=∠DAC，
∴AD是△ABC的外角∠EAC的角平分线．
点评 本题考查的是圆内接四边形的性质，掌握圆内接四边形的外角等于它的内对角是解题的关键．
练习册系列答案
相关题目
13．△ABC和△DEF分别满足下列条件，其中△ABC与△DEF不相似的是（ ）
| A． | ∠A=∠D=45°，∠C=26°，∠E=109° | |
| B． | AB=1，AC=1.5，BC=2，DE=8，DF=12，EF=16 | |
| C． | AB=a，BC=b，AC=c，DE=$\sqrt{a}$，EF=$\sqrt{b}$，DF=$\sqrt{c}$ | |
| D． | AB=AC，DE=DF，∠A=∠D=40° |
实数a，b，c在数轴上的对应点如图所示，化简a+|a+b|-|b-c|-|b+c-a|=b-a．