题目内容
5.先化简,再求值:($\frac{x+2}{x-2}$-1)÷$\frac{2x}{{x}^{2}-4}$,其中x=|$\sqrt{18}$-2|-4sin45°-(-$\frac{1}{2}$)-1.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,求出x的值代入计算即可求出值.
解答 解:原式=$\frac{x+2-(x-2)}{x-2}$•$\frac{(x+2)(x-2)}{2x}$=$\frac{4}{x-2}$•$\frac{(x+2)(x-2)}{2x}$=$\frac{2x+4}{x}$,
当x=|$\sqrt{18}$-2|-4sin45°-(-$\frac{1}{2}$)-1=3$\sqrt{2}$-2-2$\sqrt{2}$+2=$\sqrt{2}$时,原式=2+2$\sqrt{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.某校九年级(1)班的60名同学为希望工程踊跃捐款.有15人每人捐30元、14人每人捐100元、10人每人捐70元、21人每人捐50元.在这次每人捐款的数值中,中位数是( )
| A. | 30 | B. | 40 | C. | 50 | D. | 60 |
10.为了调查某班的学生每天零花钱的数量,张华随机调查了20名同学,结果如下表:则这20名同学每天使用的零花钱的众数和中位数分别是( )
| 每天使用零钱/元 | 1 | 2 | 3 | 4 | 5 |
| 人数 | 1 | 3 | 6 | 5 | 5 |
| A. | 5,3 | B. | 4,3.5 | C. | 3,3.5 | D. | 2,3 |
17.已知点A(x1,y1),B(x2,y2)是反比例函数y=$\frac{5}{x}$图象上的点,若x1>0>x2,则一定成立的是( )
| A. | y1>0>y2 | B. | y1>y2>0 | C. | 0>y1>y2 | D. | y2>0>y1 |
14.我们黑龙江冬天有一种特别的水果--冻梨.齐齐水果商店对销售的五箱冻进行了质量抽查,结果分别为:18,20,21,18,19(单位:kg),则这五箱梨质量的中位数和众数分别为( )
| A. | 20和18 | B. | 20和19 | C. | 18和18 | D. | 19和18 |
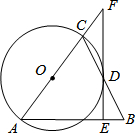 如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线EF,交AB和AC的延长线于E、F.
如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线EF,交AB和AC的延长线于E、F.