题目内容
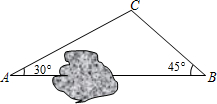 (2013•呼和浩特)如图,A、B两地之间有一座山,汽车原来从A地到B地经过C地沿折线A→C→B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10千米,∠A=30°,∠B=45°.则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果保留根号)
(2013•呼和浩特)如图,A、B两地之间有一座山,汽车原来从A地到B地经过C地沿折线A→C→B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10千米,∠A=30°,∠B=45°.则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果保留根号)分析:过C作CD⊥AB于D,在Rt△ACD中,根据AC=10,∠A=30°,解直角三角形求出AD、CD的长度,然后在Rt△BCD中,求出BD、BC的长度,用AC+BC-(AD+BD)即可求解.
解答:解:过C作CD⊥AB于D,
在Rt△ACD中,
∵AC=10,∠A=30°,
∴DC=ACsin30°=5,
AD=ACcos30°=5
,
在Rt△BCD中,
∵∠B=45°,
∴BD=CD=5,BC=5
,
则用AC+BC-(AD+BD)=10+5
-(5
+5)=5+5
-5
(千米).
答:汽车从A地到B地比原来少走(5+5
-5
)千米.

在Rt△ACD中,
∵AC=10,∠A=30°,
∴DC=ACsin30°=5,
AD=ACcos30°=5
| 3 |
在Rt△BCD中,
∵∠B=45°,
∴BD=CD=5,BC=5
| 2 |
则用AC+BC-(AD+BD)=10+5
| 2 |
| 3 |
| 2 |
| 3 |
答:汽车从A地到B地比原来少走(5+5
| 2 |
| 3 |
点评:本题考查了解直角三角形的应用,难度适中,解答本题的关键是作三角形的高建立直角三角形幷解直角三角形.

练习册系列答案
相关题目
 (2013•呼和浩特)如图,CD=CA,∠1=∠2,EC=BC,求证:DE=AB.
(2013•呼和浩特)如图,CD=CA,∠1=∠2,EC=BC,求证:DE=AB.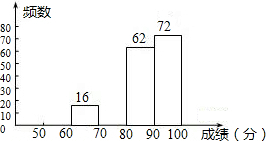 (2013•呼和浩特)某区八年级有3000名学生参加“爱我中华知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况,从中抽取了200名学生的得分进行统计.
(2013•呼和浩特)某区八年级有3000名学生参加“爱我中华知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况,从中抽取了200名学生的得分进行统计.