题目内容
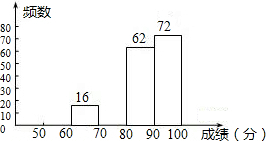 (2013•呼和浩特)某区八年级有3000名学生参加“爱我中华知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况,从中抽取了200名学生的得分进行统计.
(2013•呼和浩特)某区八年级有3000名学生参加“爱我中华知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况,从中抽取了200名学生的得分进行统计.请你根据不完整的表格,回答下列问题:
| 成绩x(分) | 频数 | 频率 |
| 50≤x<60 | 10 | 0.05 0.05 |
| 60≤x<70 | 16 | 0.08 |
| 70≤x<80 | 40 40 |
0.2 |
| 80≤x<90 | 62 | 0.31 0.31 |
| 90≤x<100 | 72 | 0.36 |
(2)若将得分转化为等级,规定50≤x<60评为“D”,60≤x<70评为“C”,70≤x<90评为“B”,90≤x<100评为“A”.这次全区八年级参加竞赛的学生约有多少学生参赛成绩被评为“D”?如果随机抽查一名参赛学生的成绩等级,则这名学生的成绩等级哪一个等级的可能性大?请说明理由.
分析:(1)由60≤x<70分数段的人数除以所占的百分比,求出总人数,进而求出70≤x<80分数段的频数,以及80≤x<90分数段的频率,补全表格即可;
(2)找出样本中评为“D”的百分比,估计出总体中“D”的人数即可;求出等级为A、B、C、D的概率,表示大小,即可作出判断.
(2)找出样本中评为“D”的百分比,估计出总体中“D”的人数即可;求出等级为A、B、C、D的概率,表示大小,即可作出判断.
解答:解:(1)根据题意得:16÷0.08=200(人),
则70≤x<80分数段的频数为200-(10+16+62+72)=40(人),50≤x<60分数段频率为0.05,80≤x<90分数段的频率为0.31,补全条形统计图,如图所示:
 ;
;
故答案为:0.05;40;0.31;
(2)由表格可知:评为“D”的频率是
=
,由此估计全区八年级参加竞赛的学生约有
×3000=150(人)被评为“D”;
∵P(A)=0.36;P(B)=0.51;P(C)=0.08;P(D)=0.05,
∴P(B)>P(A)>P(C)>P(D),
∴随机调查一名参数学生的成绩等级“B”的可能性较大.
则70≤x<80分数段的频数为200-(10+16+62+72)=40(人),50≤x<60分数段频率为0.05,80≤x<90分数段的频率为0.31,补全条形统计图,如图所示:
 ;
;故答案为:0.05;40;0.31;
(2)由表格可知:评为“D”的频率是
| 10 |
| 200 |
| 1 |
| 20 |
| 1 |
| 20 |
∵P(A)=0.36;P(B)=0.51;P(C)=0.08;P(D)=0.05,
∴P(B)>P(A)>P(C)>P(D),
∴随机调查一名参数学生的成绩等级“B”的可能性较大.
点评:此题考查了频数(率)分布直方图,频数(率)分布表,以及可能性大小,弄清题意是解本题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
 (2013•呼和浩特)如图,CD=CA,∠1=∠2,EC=BC,求证:DE=AB.
(2013•呼和浩特)如图,CD=CA,∠1=∠2,EC=BC,求证:DE=AB.