题目内容
1.若实数a、b、c满足$\sqrt{b-3a+3}$+|a+b-2|=$\sqrt{c-2}$+$\sqrt{2-c}$,则$\sqrt{{a}^{2}+{b}^{2}+{c}^{2}}$的值为$\frac{7\sqrt{2}}{4}$.分析 直接利用二次根式以及绝对值的性质得出a,b,c的值,进而化简求出答案.
解答 解:∵$\sqrt{b-3a+3}$+|a+b-2|=$\sqrt{c-2}$+$\sqrt{2-c}$,
∴c=2,且$\left\{\begin{array}{l}{a+b-2=0}\\{b-3a+3=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{5}{4}}\\{b=\frac{3}{4}}\end{array}\right.$,
则$\sqrt{{a}^{2}+{b}^{2}+{c}^{2}}$=$\sqrt{(\frac{5}{4})^{2}+(\frac{3}{4})^{2}+{2}^{2}}$
=$\frac{7\sqrt{2}}{4}$.
故答案为:$\frac{7\sqrt{2}}{4}$.
点评 此题主要考查了二次根式有意义的条件,正确得出a,b,c的值是解题关键.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目

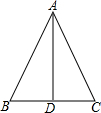 如图,在△ABC中,AB=AC,AD是BC边上的中线,则∠BDA=90°.
如图,在△ABC中,AB=AC,AD是BC边上的中线,则∠BDA=90°.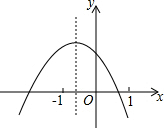 二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a<0;②c>0;③b2-4ac>0;④a+b+c>0.其中正确结论的序号是①②③(把所有正确结论的序号都填在横线上)
二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a<0;②c>0;③b2-4ac>0;④a+b+c>0.其中正确结论的序号是①②③(把所有正确结论的序号都填在横线上)