题目内容
已知:如图,⊙O与⊙A相交于C,D两点,A,O分别是两圆的圆心,△ABC内接于⊙O,弦CD交AB 于点G,交⊙O的直径AE于点F,连接BD.
于点G,交⊙O的直径AE于点F,连接BD.(1)求证:△ACG∽△DBG;
(2)求证:AC2=AG•AB;
(3)若⊙A,⊙O的直径分别为6
| 5 |
分析:(1)由圆周角定理知,∠CAG=∠BDG,由对顶角的概念知,∠AGC=∠DGB,故△ACG∽△DBG;
(2)由连心线垂直于公共弦和垂径定理知,弧AC=弧AD,由圆周角定理知∠ACG=∠ABC,而∠CAG=∠BAC,故△ACG∽△ABC.有
=
,即AC2=AG•AB.
(3)连接CE,易得Rt△CFA∽Rt△ECA,则有
=
,求得AF的值,由勾股定理求得CF的值后,由已知CG:CD=1:4,求得CG,DG的值,再在Rt△AFG中,由勾股定理求得AG的值,由2中的AC2=AG•AB,由1中的△ACG∽△DBG得到
=
,代入对应的边的值,即可求得AB,BD的值.
(2)由连心线垂直于公共弦和垂径定理知,弧AC=弧AD,由圆周角定理知∠ACG=∠ABC,而∠CAG=∠BAC,故△ACG∽△ABC.有
| AC |
| AB |
| AG |
| AC |
(3)连接CE,易得Rt△CFA∽Rt△ECA,则有
| AC |
| AE |
| AF |
| AC |
| AC |
| DB |
| AG |
| DG |
解答: (1)证明:在△ACG和△DBG中,
(1)证明:在△ACG和△DBG中,
∵∠CAG=∠BDG,∠AGC=∠DGB,
∴△ACG∽△DBG.
(2)证明:连接AD,则AC=AD.
在△ACG和△ABC中,
∵AC=AD,
∴∠ACG=∠ABC.
又∵∠CAG=∠BAC,
∴△ACG∽△ABC.
∴
=
,即AC2=AG•AB.
(3)解:连接CE,则∠ACE=90°.
∵⊙O与⊙A相交于C,D两点,
∴圆心O,A在弦CD的垂直平分线上,即AO垂直平分弦CD.
∴CF=DF,CF⊥AE且
=
.
∵⊙A,⊙O的直径分别为6
,15,
∴AC=3
,AE=15.
在Rt△CFA和Rt△ECA中,
∵∠ACF=∠ADC=∠AEC,
∴Rt△CFA∽Rt△ECA.
∴
=
,即AF=
=
=3.
在Rt△AFC中,由勾股定理,得AC2=AF2+CF2,
即(3
)2=32+CF2.解得CF=6(舍去负值).
∵CG:CD=1:4,且CD=2CF=12,
∴CG:DG=1:3,
∴CG=FG=12×
=3,DG=12×
=9.
在Rt△AFG中,由勾股定理,得AG2=AF2+FG2=32+32=18,
∴AG=3
(舍去负值).
由(2),有AC2=AG•AB,即(3
)2=3
•AB.
解得AB=
.
由(1),有△ACG∽△DBG,得
=
.
∴BD=
=
=
.
 (1)证明:在△ACG和△DBG中,
(1)证明:在△ACG和△DBG中,∵∠CAG=∠BDG,∠AGC=∠DGB,
∴△ACG∽△DBG.
(2)证明:连接AD,则AC=AD.
在△ACG和△ABC中,
∵AC=AD,
∴∠ACG=∠ABC.
又∵∠CAG=∠BAC,
∴△ACG∽△ABC.
∴
| AC |
| AB |
| AG |
| AC |
(3)解:连接CE,则∠ACE=90°.
∵⊙O与⊙A相交于C,D两点,
∴圆心O,A在弦CD的垂直平分线上,即AO垂直平分弦CD.
∴CF=DF,CF⊥AE且
 |
| AC |
 |
| AD |
∵⊙A,⊙O的直径分别为6
| 5 |
∴AC=3
| 5 |
在Rt△CFA和Rt△ECA中,
∵∠ACF=∠ADC=∠AEC,
∴Rt△CFA∽Rt△ECA.
∴
| AC |
| AE |
| AF |
| AC |
| AC2 |
| AE |
(3
| ||
| 15 |
在Rt△AFC中,由勾股定理,得AC2=AF2+CF2,
即(3
| 5 |
∵CG:CD=1:4,且CD=2CF=12,
∴CG:DG=1:3,
∴CG=FG=12×
| 1 |
| 4 |
| 3 |
| 4 |
在Rt△AFG中,由勾股定理,得AG2=AF2+FG2=32+32=18,
∴AG=3
| 2 |
由(2),有AC2=AG•AB,即(3
| 5 |
| 2 |
解得AB=
15
| ||
| 2 |
由(1),有△ACG∽△DBG,得
| AC |
| DB |
| AG |
| DG |
∴BD=
| AC•DG |
| AG |
3
| ||
3
|
9
| ||
| 2 |
点评:本题是圆内的一道综合题,利用了连心线与公共弦的关系,圆周角定理,垂径定理,直径对的圆周角是直角,中垂线的性质,勾股定理,相似三角形的判定和性质求解.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.
21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.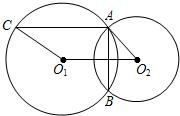 ,⊙O2的半径为
,⊙O2的半径为 14、已知:如图,⊙O1与⊙O2外切于点P,⊙O1的半径为3,且O1O2=8,则⊙O2的半径R=
14、已知:如图,⊙O1与⊙O2外切于点P,⊙O1的半径为3,且O1O2=8,则⊙O2的半径R= (1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D.
(1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D. 已知:如图,⊙O1与⊙O2相交于A,B两点.求证:直线O1O2垂直平分AB.
已知:如图,⊙O1与⊙O2相交于A,B两点.求证:直线O1O2垂直平分AB.