题目内容
如图：O为△ABC两边高线的交点，连OB、OC，若∠ABC=50°，∠ACB=70°，则∠BOC=
- A.100°
- B.130°
- C.120°
- D.115°
C
分析：因为是高线的交点，所以能分别求出∠OCB和∠OBC的度数，从而能求出∠BOC的度数．
解答：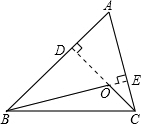
解：延长CO交AB于D，延长BO交AC于E．
∵∠BEC=90°，∠ACB=70°，
∴∠OBC=20°，
∵∠BDC=90°，∠ABC=50°，
∴∠OCB=40°，
∴∠BOC=180°-20°-40°=120°．
故选C．
点评：本题考查三角形的内角和定理，关键知道内角和为180°，反复用可求出结果．
分析：因为是高线的交点，所以能分别求出∠OCB和∠OBC的度数，从而能求出∠BOC的度数．
解答：
解：延长CO交AB于D，延长BO交AC于E．∵∠BEC=90°，∠ACB=70°，
∴∠OBC=20°，
∵∠BDC=90°，∠ABC=50°，
∴∠OCB=40°，
∴∠BOC=180°-20°-40°=120°．
故选C．
点评：本题考查三角形的内角和定理，关键知道内角和为180°，反复用可求出结果．
练习册系列答案
相关题目
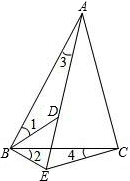如图，D为△ABC内一点，E为△ABC外一点，且∠1=∠2，∠3=∠4，找出图中的两对相似三角形并说明理由．
认真阅读，并回答下面问题：
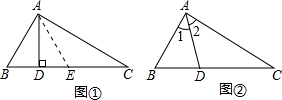我们知道，利用三角形全等可以证明两条线段相等．但是我们会碰到这样的“和差”问题：“如图①，AD为△ABC的高，∠ABC=2∠C，证明：CD=AB+BD”．我们可以用“截长、补短”的方法将这类问题转化为证明两条线段相等的问题：在CD上截取DE=BD，连结AE．