题目内容

9．先化简，再求值：（x+3）（x-1）+（x+2）（x-2）-2（x-1）2，其中x=$\frac{1}{2}$．

分析 先算乘法，再合并同类项，最后代入求出即可．

解答 解：（x+3）（x-1）+（x+2）（x-2）-2（x-1）2
=x2-x+3x-3+（x2-4）-2（x2-2x+1）
=x2-x+3x-3+x2-4-2x2+4x-2
=6x-9，
当x=$\frac{1}{2}$时，6x-9=6×$\frac{1}{2}$-9=-6．

点评 本题考查了整式的混合运算和求值的应用，能正确运用整式的运算法则进行化简是解此题的关键，注意运算顺序．

练习册系列答案
相关题目
19．已知$\left\{\begin{array}{l}{x=3}\\{y=-4}\end{array}\right.$是方程ax-2y=2的一个解，则a的值为（　　）
A．-2B．2C．$\frac{10}{3}$D．-$\frac{10}{3}$
20．青山村种的水稻2009年平均每公顷产7500千克，2011年平均每公顷产9075千克，求水稻每公顷产量的年平均增长率．
17．计算题：
（1）计算：$\sqrt{32}-2\sqrt{12}-\sqrt{27}+\sqrt{8}$
（2）计算：3${\;}^{-2}+\sqrt{16}-（π-1）^{0}+|-\frac{8}{9}$|
（3）解方程组：$\left\{\begin{array}{l}{3x-y=7}\\{5x+2y=8}\end{array}$．
4．如图，矩形纸片按图（1）中的虚线第一次折叠得图（2），折痕与矩形一边的形成的∠1=65°，再按图（2）中的虚线进行第二折叠得到图（3），则∠2的度数为（　　）
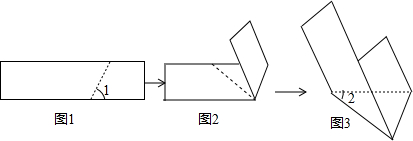
A．20°B．25°C．30°D．35°
14．阅读材料：
方程x2-x-2=0中，只含有一个未知数且未知数的次数为2．像这样的方程叫做一元二次方程．把方程的左边分解因式得到（x-2）（x+1）=0．我们知道两个因式乘积为0，其中有一个因式为0即可，因此方程可以转化为：x-2=0或       x+1=0
解这两个一次方程得：x=2或x=-1．
所以原方程的解为：x=2或x=-1．
上述将方程x2-x-2=0转化为x-2=0或x+1=0的过程，是将二次降为一次的“降次”过程，从而使得问题得到解决．
仿照上面降次的方法，解决下列问题：
（1）解方程x2-3x=0
（2）解方程组：$\left\{\begin{array}{l}{x^2}-9{y^2}=0\\ x+y=4\end{array}\right.$
知识迁移：
根据有理数的乘法法则“两数相乘，异号得负”，尝试解不等式：（x-3）（x+1）＜0．
1．下列运算正确的是（　　）
A．a2•a3=a6B．（ab）3=ab3C．（a2）3=a6D．a6÷a2=a3
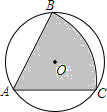18．如图，有一直径为4的圆形铁皮，要从中剪出一个最大圆心角为60°的扇形ABC．那么剪下的扇形ABC（阴影部分）的面积为2π；用此剪下的扇形铁皮围成一个圆锥，该圆锥的底面圆的半径r=$\frac{{\sqrt{3}}}{3}$．
19．拼图是一种数学实验，我们利用硬纸板拼图，不仅可以探索整式乘法与因式分解之间的内在联系，还可以利用同一图形不同的面积表示方法来探索新的结论．
（1）观察下面图①的硬纸板拼图，写出一个表示相等关系的式子：（2a+b）（a+b）=2a2+3ab+b2．
（2）用不同的方法表示图②中阴影部分的面积，可以得到的乘法公式为（a+b）（a-b）=a2-b2．
（3）两个边长为a，b，c的直角三角形硬纸板和一个两条直角边都是c的直角三角形硬纸板拼成图③，用不同的方法计算这个图形的面积．你能发现a，b，c之间具有怎样的相等关系？（用最简形式表示）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网