Question

我们知道：15°角可以看做是60°角与45°角的差．请借助有一个内角是60°的直角三角形和等腰直角三角形构造出一个图形并借助它求出sin15°的值 （要求画出构造的图形）．

Answer 1

解：如图，△ABC为有一个内角为60°的直角三角形，△ADC为等腰直角三角形，所以∠DAB=15°．
作DE⊥AB，垂足为E．
设DC=1，则AC=1，由勾股定理AD=，
由∠BAC=60°可得AB=2，BC=，
则BD=-1，
在Rt△BED中，∠B=30°，
则DE=，
在Rt△DEA中，sin∠DAE==．
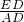即sin15°=．
分析：作DE⊥AB，垂足为E．设DC=1，则AC=1，由勾股定理AD=，根据三角函数可得DE=，再根据正弦的定义即可求解．
点评：考查了解直角三角形，本题的关键是得到15°的正弦所对的直角边和斜边的长度．