题目内容
设a、b、c均为正整数,若
<
<
,则a、b、c的大小是( )
| c |
| a+b |
| a |
| b+c |
| b |
| c+a |
| A、a>b>c |
| B、b>a>c |
| C、a>c>b |
| D、c>a>b |
分析:首先根据a、b、c均为正整数,确定a+b、b+c、a+c、a+b+c也为正整数,再通过
<
<
分为
<
、
<
、
<
分别通过去分式,因式分解,判断出b>c、b>a、a>c,综合得出b>a>c
| c |
| a+b |
| a |
| b+c |
| b |
| c+a |
| c |
| a+b |
| b |
| c+a |
| a |
| b+c |
| b |
| c+a |
| c |
| a+b |
| a |
| b+c |
解答:解:∵a、b、c均为正整数,
∴a+b、b+c、a+c、a+b+c也为正整数,
∵
<
<
,
∴
<
,
?c2+ac<b2+ab,
?b2-c2+ab-ac>0,
?(b-c)(a+b+c)>0,
?b>c,
<
,
?ac+a2<b2+bc,
?b2-a2+bc-ac>0,
?(b+a)(b-a)+c(b-a)>0,
?(b-a)(a+b+c)>0,
?b>a,
<
,
?a2+ab>bc+c2,
?a2+ab-bc-c2>0,
?(a+c)(a-c)+b(a-c)>0,
?(a-c)(a+b+c)>0,
?a>c,
综上,c<a<b.
故选B.
∴a+b、b+c、a+c、a+b+c也为正整数,
∵
| c |
| a+b |
| a |
| b+c |
| b |
| c+a |
∴
| c |
| a+b |
| b |
| c+a |
?c2+ac<b2+ab,
?b2-c2+ab-ac>0,
?(b-c)(a+b+c)>0,
?b>c,
| a |
| b+c |
| b |
| c+a |
?ac+a2<b2+bc,
?b2-a2+bc-ac>0,
?(b+a)(b-a)+c(b-a)>0,
?(b-a)(a+b+c)>0,
?b>a,
| c |
| a+b |
| a |
| b+c |
?a2+ab>bc+c2,
?a2+ab-bc-c2>0,
?(a+c)(a-c)+b(a-c)>0,
?(a-c)(a+b+c)>0,
?a>c,
综上,c<a<b.
故选B.
点评:本题主要考查分式的混合运算,因式分解是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则a、b、c的大小是
,则a、b、c的大小是 =
=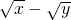 ,则x+y+M的值是 ________.
,则x+y+M的值是 ________.