题目内容
1．设α、β是方程x2+x-2017=0的两个实数根，则α2+2α+β的值为2016．分析 根据根与系数的关系以及一元二次方程的解可得出α+β=-1、α2+α=2017，将其代入α2+2α+β=α2+α+α+β中即可求出结论．
解答 解：∵α、β是方程x2+x-2017=0的两个实数根，
∴α+β=-1，α2+α=2017，
∴α2+2α+β=α2+α+α+β=2017-1=2016．
故答案为：2016．
点评 本题考查了根与系数的关系以及一元二次方程的解，根据根与系数的关系以及一元二次方程的解可得出α+β=-1、α2+α=2017是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
11．
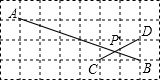如图，在边长相同的小正方形组成的网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD交于点P，则tan∠APC的值是（ ）
如图，在边长相同的小正方形组成的网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD交于点P，则tan∠APC的值是（ ）| A． | $\frac{2}{3}$ | B． | 1 | C． | 2 | D． | $\frac{\sqrt{3}}{2}$ |
12．下列能判定△ABC为等腰三角形的是（ ）
| A． | ∠A=50°，∠B=40° | B． | ∠A=70°，∠B=40° | ||
| C． | AB=AC=4，BC=8 | D． | AB=3，BC=8，周长为16 |
如图，AC、BD、EF相交于O，若OA=OC，OB=OD，OE=OF，则图中共有全等三角形3对．