题目内容
如图,四边形ABCD中,AC平分∠BAD ,CE⊥AB于E,AD+AB=2AE.求证:∠B+∠ADC=180°.
,CE⊥AB于E,AD+AB=2AE.求证:∠B+∠ADC=180°.
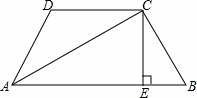
∠B+∠ADC=180°.
详解:延长AD,过C作CF垂直AD的延长线于点F,
∵AC平分∠BAD,
∴∠FAC=∠EAC,
∵CE⊥AB,CF⊥AD,
∴∠DFC=∠CEB=90°,
∴△AFC≌△AEC,
∴AF=AE,CF=CE,
∵2AE=AB+AD,
又∵AD=AFDF,AB=AE+BE,AF=AE,
∴2AE=AE+BE+AEDF,
∴BE=DF,
∵∠DFC=∠CEB=90°,CF=CE,
∴△CDF≌△CEB,
∴∠ABC=∠CDF,
∵∠ADC+∠CDF=180°,
∴∠B+∠ADC=180°.


练习册系列答案
相关题目
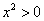 ,那么
,那么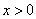 .
. B于E,交BC于F,DG为AC的垂直平分线
B于E,交BC于F,DG为AC的垂直平分线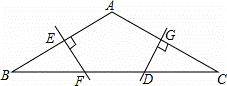
 C上任意一点(M与A不重合)MD⊥BC,交∠BAC的平分线于点D,求证:MD=MA.
C上任意一点(M与A不重合)MD⊥BC,交∠BAC的平分线于点D,求证:MD=MA.
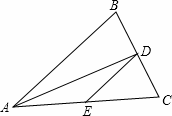
 中,AD是∠BAC的平分线.请证明:AB:AC=BD:CD.
中,AD是∠BAC的平分线.请证明:AB:AC=BD:CD.
 是最小的自然数,
是最小的自然数, 是最大的负整数,
是最大的负整数, 是绝对值最小的有理数,则
是绝对值最小的有理数,则
 三个数的和为 。
三个数的和为 。