题目内容
3. 已知:在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连结AD、BE交于点P,作BQ⊥AD,垂足为Q.求证:
已知:在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连结AD、BE交于点P,作BQ⊥AD,垂足为Q.求证:(1)△ACD≌△BAE;
(2)BP=2PQ.
分析 (1)根据等边三角形的性质得AB=AC=BC,∠BAC=∠C=60°,然后根据“SAS”可证明△ACD≌△BAE;
(2)由△ACD≌△BAE得∠ABE=∠CAD,再利用三角形外角性质可计算出∠BPD=60°,然后根据含30度的直角三角形三边的关系即可得到PB=2PQ.
解答 证明:(1)∵△ABC为等边三角形,
∴AB=AC=BC,∠BAC=∠C=60°,
在△ACD和△BAE中,
$\left\{\begin{array}{l}{AB=CA}\\{∠BAE=∠ACD}\\{AE=CD}\end{array}\right.$,
∴△ACD≌△BAE;
(2)∵△ACD≌△BAE,
∴∠ABE=∠CAD,
∵∠BPD=∠ABP+∠BAP,
∴∠BPD=∠EAP+∠BAP=∠BAE=60°,
∵BQ⊥AD,
∴∠AQB=90°,
在Rt△PBQ中,∵∠PBQ=30°,
∴PQ=$\frac{1}{2}$BP,
即PB=2PQ.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.也考查了全等三角形的性质和含30度的直角三角形三边的关系.

练习册系列答案
相关题目
14.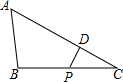 如图,在△ABC中,∠ABC>90°,∠C=30°,BC=12,P是BC上的一个动点,过点P作PD⊥AC于点D,设CP=x,△CDP的面积为y,则y与x之间的函数图象大致为( )
如图,在△ABC中,∠ABC>90°,∠C=30°,BC=12,P是BC上的一个动点,过点P作PD⊥AC于点D,设CP=x,△CDP的面积为y,则y与x之间的函数图象大致为( )
 如图,在△ABC中,∠ABC>90°,∠C=30°,BC=12,P是BC上的一个动点,过点P作PD⊥AC于点D,设CP=x,△CDP的面积为y,则y与x之间的函数图象大致为( )
如图,在△ABC中,∠ABC>90°,∠C=30°,BC=12,P是BC上的一个动点,过点P作PD⊥AC于点D,设CP=x,△CDP的面积为y,则y与x之间的函数图象大致为( )| A. | 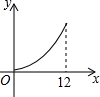 | B. | 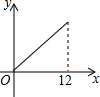 | C. | 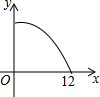 | D. | 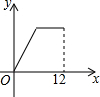 |
11.一个口袋中有红、白、黑球共10个,这些球除颜色外都相同,将口袋中的球搅拌均匀,从中随机摸出一个球,记下颜色后放回袋中.不断重复这个过程,共摸了100次球,发现有49次摸到红球,21次摸到黑球,则袋中白球大约是( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
8.法国病毒学家团队2014年3月4日宣布,他们发现了世界上第三种超大型病毒,这种巨型史前病毒直径超过0.00000025米,0.0000005用科学记数法可表示为( )
| A. | 5×10-8 | B. | 5×10-9 | C. | 0.5×10-6 | D. | 0.05×10-5 |
 如图,已知在△ABC中,点D、E分别是AB、AC上一点,且AD=AE,∠ABE=∠ACD,BE与CD相交于点F.试判断△BCF的形状,并说明理由.
如图,已知在△ABC中,点D、E分别是AB、AC上一点,且AD=AE,∠ABE=∠ACD,BE与CD相交于点F.试判断△BCF的形状,并说明理由.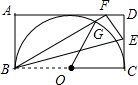 如图,在矩形ABCD中,BC=12,以BC为直径的半圆O恰好与AD相切,现将矩形ABCD沿BE折叠,使点C落在边AD的点F处,并交半圆O于点G,则扇形OCG的面积为( )
如图,在矩形ABCD中,BC=12,以BC为直径的半圆O恰好与AD相切,现将矩形ABCD沿BE折叠,使点C落在边AD的点F处,并交半圆O于点G,则扇形OCG的面积为( )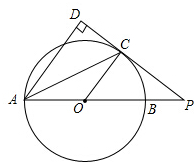 如图,AB是⊙O直径,∠DAC=∠BAC,CD⊥AD,交AB延长线于点P,
如图,AB是⊙O直径,∠DAC=∠BAC,CD⊥AD,交AB延长线于点P,