题目内容
12.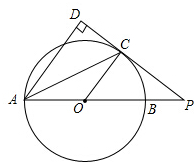 如图,AB是⊙O直径,∠DAC=∠BAC,CD⊥AD,交AB延长线于点P,
如图,AB是⊙O直径,∠DAC=∠BAC,CD⊥AD,交AB延长线于点P,(1)求证:PC是⊙O的切线;
(2)若tan∠BAC=$\frac{1}{2}$,PB=2,求⊙O半径.
分析 (1)根据等腰三角形的性质和∠DAC=∠BAC,得出∠DAC=∠OCA,判定OC∥AD,得出∠OCP=90°,即可证得结论;
(2)连接BC,证得△PBC∽△CPA,根据相似三角形的性质得出$\frac{PC}{PA}$=$\frac{CB}{AC}$=$\frac{PB}{PC}$,根据tan∠BAC=$\frac{1}{2}$得出PC2=PB•PA,PA=2PC,进一步求得PC=4,设⊙O半径为x,则OP=x+2,根据勾股定理列出方程,解方程即可求得.
解答 (1)证明:∵OA=OC,
∴∠OAC=∠OCA,又∠DAC=∠BAC,
∴∠DAC=∠OCA,
∴OC∥AD,又CD⊥AD,
∴∠OCP=90°,
∴PC是⊙O的切线;
(2)解:如图,连接BC,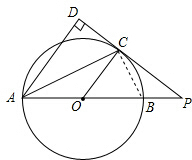 ∵PC是⊙O的切线,
∵PC是⊙O的切线,
∴∠PCB=∠PAC,
∵∠BPC=∠CPA,
∴△PBC∽△CPA,
∴$\frac{PC}{PA}$=$\frac{CB}{AC}$=$\frac{PB}{PC}$,
∵tan∠BAC=$\frac{BC}{AC}$=$\frac{1}{2}$,
∴PC2=PB•PA,PA=2PC,
∴PC2=2PB•PC,PC=2PB=4,
设⊙O半径为x,则OP=x+2,
在RT△OPC中,OP2=OC2+PC2,即(x+2)2=x2+42,
解得x=3,
∴⊙O半径为3.
点评 本题考查了切线的判定和性质三角形相似的判定和性质以及勾股定理的应用,作出辅助线构建相似三角形是解题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
4.今年要实现大病保险全覆盖,中央财政安排城乡医疗救助补助资金160亿元,160亿元这一数据用科学记数法表示为( )
| A. | 16×109元 | B. | 1.6×1010元 | C. | 0.16×1011元 | D. | 1.6×109元 |
2.下列命题中,正确的是( )
| A. | 菱形的对角线相等 | |
| B. | 平行四边形既是轴对称图形,又是中心对称图形 | |
| C. | 正方形的对角线相等且互相垂直 | |
| D. | 矩形的对角线不能相等 |
 如图,?ABCD,AB=6,AD=9,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DF的长等于( )
如图,?ABCD,AB=6,AD=9,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DF的长等于( ) 已知:在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连结AD、BE交于点P,作BQ⊥AD,垂足为Q.求证:
已知:在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连结AD、BE交于点P,作BQ⊥AD,垂足为Q.求证: 在如图所示的方格纸上过点P画直线AB的平行线,过点P作PM⊥AB于点M.
在如图所示的方格纸上过点P画直线AB的平行线,过点P作PM⊥AB于点M.