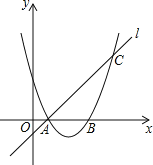题目内容
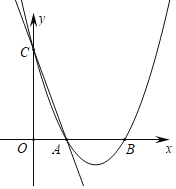
【题目】如图,抛物线![]() 与x轴交于A(-1,0),B(5,0)两点,直线
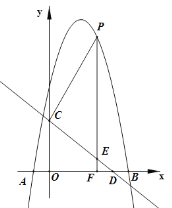
与x轴交于A(-1,0),B(5,0)两点,直线![]() 与y轴交于点C,与x轴交于点D。点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴与点F,交直线CD于点E。设点P的横坐标为m。
与y轴交于点C,与x轴交于点D。点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴与点F,交直线CD于点E。设点P的横坐标为m。
(1)求抛物线的解析式;
(2)若PF=5EF,求m的值.
【答案】(1)![]() ;(2)2或
;(2)2或![]()
【解析】
(1)利用待定系数法即可求出抛物线的解析式;
(2)用含m的代数式分别表示出PE、EF,然后列方程PE=![]() —(
—(![]() )=
)=![]() ,再分情况讨论求解即可.
,再分情况讨论求解即可.
(1)∵抛物线![]() 与x轴交于A(-1,0),B(5,0)两点,
与x轴交于A(-1,0),B(5,0)两点,
∴ 解得
解得![]()
∴抛物线的解析式为![]()
(2)点P的横坐标为m,则P(m,![]() ),E(m,
),E(m,![]() ),F(m,0)
),F(m,0)
∵点P在x轴上方,要使PE=5EF,点P应在y轴右侧,∴0<m<5
∴PE=![]() —(
—(![]() )=
)=![]()
分两种情况讨论:
①当点E在点F上方时,EF=![]() ,
,
∵PE=5EF,∴![]() =5(
=5(![]() )
)
即![]() ,解得
,解得![]() ,
,![]() (舍去)
(舍去)
②当点E在点F下方时,EF=![]()
∵PE=5EF,∴![]() =5(
=5(![]() )
)
即![]() ,解得
,解得![]() ,
,![]() (舍去)
(舍去)
∴m的值为2或![]()

练习册系列答案
相关题目