��Ŀ����
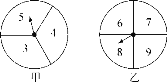
����Ŀ����һ����ѧ��ȤС���У������������λͬѧ�������ͼ��ʾ������ת������Ϸ(ÿ��ת�̱��ֳ������ȵļ������Σ�����ÿ�����������ڱ�������)����Ϸ�������£����˷ֱ�ͬʱת���ס���ת�̣�ת��ֹͣ����ָ����ָ������������С��12���������ʤ����ָ����ָ�����������͵���12����Ϊƽ�֣���ָ����ָ�����������ʹ���12����������ʤ(��ָ��ͣ�ڵȷ����ϣ���תһ�Σ�ֱ��ָ��ָ��ijһ����Ϊֹ)��
(1)�����б�����״ͼ�ķ�����ʾ��������Ϸ�������͵����п��ܵĽ����
(2)����Ϸ�Ƿ�ƽ���������ƽ��������Ϸ����ʹ��Ϸ��ƽ��
���𰸡���1��12��2������Ϸ����ƽ
��������
��1�����������г����ó���Ϸ�������͵����п��ܵĽ������
��2�����ݣ�1���ó��������е�����������к�Ϊ12���������Ϊ13����������ٸ��ݸ��ʹ�ʽ���ɵó�������Ϸ��ƽ��ʹ˫��������ͬ������
(1)�б����£�
���� | 6 | 7 | 8 | 9 |
3 | 9 | 10 | 11 | 12 |
4 | 10 | 11 | 12 | 13 |
5 | 11 | 12 | 13 | 14 |
�ɱ����֪��������12�ֵȿ��ܵĽ����
(2)��(1)��֪��������12�ֵȿ��ܵĽ�������к�С��12�Ľ����6�֣��ʹ���12�Ľ����3�֣�
�������ʤ�ĸ���Ϊ![]() ��
��![]() ��������ʤ�ĸ���Ϊ
��������ʤ�ĸ���Ϊ![]() ��
��![]() .
.
��![]() ��
��![]() ��
��
�����Ϸ����ƽ��
��ʹ��Ϸ��ƽ��������Ϸ��������(�𰸲�Ψһ)��
���˷ֱ�ͬʱת���ס���ת�̣�ת��ֹͣ����ָ����ָ������������С��12���������ʤ����ָ����ָ�����������ʹ���11����������ʤ(��ָ��ͣ�ڵȷ����ϣ���תһ�Σ�ֱ��ָ��ָ��ijһ����Ϊֹ)��

 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�����Ŀ������ʦ��1����������ɸ�����(��Щ�����ɫ�ⶼ��ͬ)����һ�������Ŀڴ������ȣ�������ѧ����������ʵ�飬ÿ������1����(�зŻ�)���±��ǻ�����е�һ��ͳ������.
����Ĵ���n | 100 | 150 | 200 | 500 | 800 | 1000 |
��������Ĵ���m | 23 | 31 | 60 | 130 | 203 | 251 |
���������Ƶ�� | 0.23 | 0.207 | 0.30 | 0.26 | 0.254 | 0.251 |
(1)�����ϱ����ݹ��ƴӴ�������1�����Ǻ���ĸ�����_________��
(2)���ƴ��а���ĸ�����