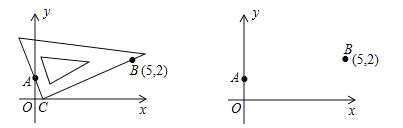题目内容
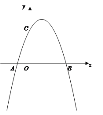
【题目】已知:如图,直线![]() 的函数解析式为
的函数解析式为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
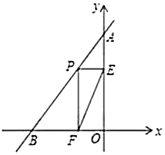
(1)直接写出点![]() 的坐标________;
的坐标________;![]() 点的坐标________;
点的坐标________;
(2)若点![]() 为线段
为线段![]() 上的一个动点,作
上的一个动点,作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,连接
,连接![]() ,问:①若
,问:①若![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式;②直接写出
的函数关系式;②直接写出![]() 的最小值________;
的最小值________;
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() (
(![]() ),②
),②![]()
【解析】
(1)令![]() 求出y的值,即可得到A的坐标,令
求出y的值,即可得到A的坐标,令![]() 求出x的值,即可得到B的坐标;
求出x的值,即可得到B的坐标;
(2)①直接利用三角形的面积公式![]() 以及a,b之间的关系
以及a,b之间的关系![]() 即可得到
即可得到![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②易证四边形PEOF是矩形,然后利用勾股定理得出![]() ,然后可得到
,然后可得到![]() 的最小值,从而即可确定EF的最小值.
的最小值,从而即可确定EF的最小值.
(1)令![]() ,
,![]() ,则点A的坐标为
,则点A的坐标为![]() ;
;
令![]() ,即
,即![]() ,解得
,解得![]() ,则点B的坐标为
,则点B的坐标为![]() ;
;
(2)①连接PO,

∵点B的坐标为![]() ,
,
∴![]() .
.
∵点![]() 为线段
为线段![]() 上的一个动点,
上的一个动点,
∴![]() .
.
∵![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,
∴![]() ,
,
∴![]() (
(![]() );
);
②∵![]() 轴,
轴,![]() 轴,
轴,![]() ,
,
∴四边形PEOF是矩形,
∴![]() .
.
在![]() 中,
中,
![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() 的最小值为20.
的最小值为20.
∵![]() ,
,
∴EF的最小值为![]() .
.

练习册系列答案
相关题目