题目内容
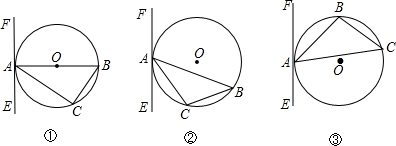
如图，点D、B分别在∠A的两边上，C是∠DAB内一点，AB=AD，BC=CD，CE⊥AD于E，CF⊥AF于F，求证：CE=CF．
考点：全等三角形的判定与性质,角平分线的性质
专题：证明题
分析：首先证明△ADC≌△ABC可得∠DAC=∠BAC，再根据角平分线的性质：角的平分线上的点到角的两边的距离相等可得结论．
解答：证明：在△ADC和△ABC中，
，
∴△ADC≌△ABC（SSS），
∴∠DAC=∠BAC，
∵CE⊥AD于E，CF⊥AF于F，
∴CE=CF．
|
∴△ADC≌△ABC（SSS），
∴∠DAC=∠BAC，
∵CE⊥AD于E，CF⊥AF于F，
∴CE=CF．
点评：此题主要考查了全等三角形的判定与性质以及角平分线的性质，关键是掌握全等三角形的判定方法．
练习册系列答案
轻松暑假总复习系列答案
相关题目
如图，在△ABC中，AB=AC，BC=8，AD平分∠BAC，则BD=
如图，⊙O是△ABC的
如图，在Rt△ABC中，锐角A的