题目内容
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() .
.
(1)求抛物线解析式及![]() 点坐标;
点坐标;
(2)连接![]() ,求
,求![]() 的面积;
的面积;
(3)若点![]() 为抛物线上一动点,连接
为抛物线上一动点,连接![]() ,当点
,当点![]() 运动到某一位置时,
运动到某一位置时,![]() 面积为
面积为![]() 的面积的
的面积的![]() 倍,求此时点
倍,求此时点![]() 的坐标.
的坐标.
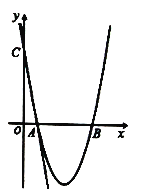
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 点的坐标为
点的坐标为![]() ,
,![]()
![]() ,
,![]() ,见解析.
,见解析.
【解析】
(1)利用![]() 两点是一次函数上的点求出
两点是一次函数上的点求出![]() 两点,再代入二次函数求解即可.
两点,再代入二次函数求解即可.
(2)根据![]() ,
,![]() 求出
求出![]() ,求出△ABC.
,求出△ABC.
(3)根据![]() 面积为
面积为![]() 的面积的
的面积的![]() 倍,求出
倍,求出![]() ,得出
,得出![]() 求出此时M的坐标即可.
求出此时M的坐标即可.
(1)解:∵直线![]()
∴令![]() ,则
,则![]() ,解得
,解得![]()
∴![]()
令![]() ,则
,则![]() ,∴
,∴![]()
将点![]() ,
,![]() 代入
代入![]() 中得,
中得,
![]() ,解得
,解得![]()
∴抛物线的解析式为:![]() ;
;
令![]() ,则
,则![]() ,解得
,解得![]()
∴![]() .
.
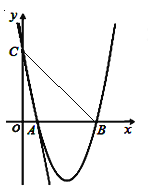
(2)解:∵![]() ,
,![]() ∴
∴![]()
∴![]()
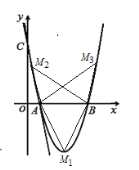
(3)∵![]() 面积为
面积为![]() 的面积的
的面积的![]() 倍,
倍,
∴![]()
∵AB=4 ,
∴![]() ,
,
∵![]()
∴抛物线的顶点坐标为![]() 符合条件,
符合条件,
当![]() 时,
时,![]() ,解的,x1=
,解的,x1=![]() ,x
,x![]() ,
,
∴![]() 点的坐标为
点的坐标为![]() (3,-4),
(3,-4),![]()
![]() ,
,![]()
![]() .
.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
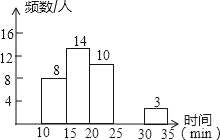
【题目】某校中午学生用餐比较拥挤,为建议学校分年级错时用餐,李老师带领数学学习小组在某天随机调查了部分学生,统计了他们从下课到就餐结束所用的时间,并绘制成统计表和如图所示的不完整统计图.
根据以上提供的信息,解答下列问题:
(1)表中a=_____,b=_____,c=_____,补全频数分布直方图;
(2)此次调查中,中位数所在的时间段是_____min.
时间分段/min | 频(人)数 | 百分比 |
10≤x<15 | 8 | 20% |
15≤x<20 | 14 | a |
20≤x<25 | 10 | 25% |
25≤x<30 | b | 12.50% |
30≤x<35 | 3 | 7.50% |
合计 | c | 100% |
(3)这所学校共有1200人,试估算从下课到就餐结束所用时间不少于20min的共有多少人?