题目内容
已知AB为⊙O的直径,P为AB弧的中点.
(1)若⊙O′与⊙O外切于点P(见图9-17甲),AP,BP的延长线分别交⊙O′于点C、D,连结CD,则△PCD是_____________三角形;
(2)⊙O′与⊙O相交于点P,Q(见图9-17乙),连结AQ、BQ并延长分别交⊙O′于点E、F,请选择下列两个问题中的一个作答:
问题一:判断△PEF的形状,并证明你的结论;
问题二:判断线段AE与BF的关系,并证明你的结论.
我选择问题________![]() _____________________,结论:_______________________________.
_____________________,结论:_______________________________.
证明:
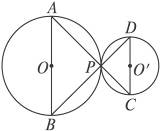
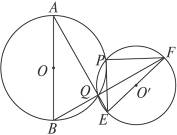
甲 乙
图9-17
解:(1)等腰直角.

甲
(2)问题一:△PEF是等腰直角三角形.
证明:连结PA、PB.
∵AB是直径,
∴∠AQB=∠EQF=90°.
∴EF是⊙O′的直径.∴∠EPF=90°.
在△APE和△BPF中,
∵PA=PB,∠PBF=∠PAE,![]()
∠APE=∠BPF=90°+∠EPB,
∴△APE≌△BPF.
∴PE=PF.∴△PEF是等腰直角三角形.
问题二:连结PA、PB.
由(1)可证△APE≌△BPF,∴AE=BF.
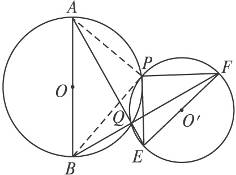
乙
提示:直径所对的圆周角是直![]() 角,并通过对顶角将两个圆中的相关量联系起来.
角,并通过对顶角将两个圆中的相关量联系起来.
答案:247.2厘米

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°.
如图,已知AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°. 22、如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是( )
22、如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是( )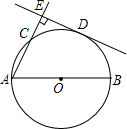 如图所示,已知AB为⊙O的直径,C、D是直径AB同侧圆周上两点,且弧CD=弧BD,过D作DE⊥AC于点E,求证:DE是⊙O的切线.
如图所示,已知AB为⊙O的直径,C、D是直径AB同侧圆周上两点,且弧CD=弧BD,过D作DE⊥AC于点E,求证:DE是⊙O的切线. (2013•沙市区一模)如图,已知AB为⊙O的直径,PA与⊙O相切与点A,线段OP与弦AC垂直并相交于点D,OP与⊙O相交于点E,连接BC.
(2013•沙市区一模)如图,已知AB为⊙O的直径,PA与⊙O相切与点A,线段OP与弦AC垂直并相交于点D,OP与⊙O相交于点E,连接BC. 已知AB为半圆的直径,弦AD、BC相交于M,点E在AM上,且∠CEM=∠B,AB=1,则cos∠AMC的值等于线段( )的长.
已知AB为半圆的直径,弦AD、BC相交于M,点E在AM上,且∠CEM=∠B,AB=1,则cos∠AMC的值等于线段( )的长.