题目内容
 如图,已知AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°.
如图,已知AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°.(Ⅰ)求∠P的大小;
(Ⅱ)若AB=2,求PA的长(结果保留根号).
分析:(Ⅰ)根据切线的性质及切线长定理可证明△PAC为等边三角形,则∠P的大小可求;
(Ⅱ)由(Ⅰ)知PA=PC,在Rt△ACB中,利用30°的特殊角度可求得AC的长.
(Ⅱ)由(Ⅰ)知PA=PC,在Rt△ACB中,利用30°的特殊角度可求得AC的长.
解答:解:(Ⅰ)∵PA是⊙O的切线,AB为⊙O的直径,
∴PA⊥AB,
∴∠BAP=90°;
∵∠BAC=30°,
∴∠CAP=90°-∠BAC=60°.
又∵PA、PC切⊙O于点A、C,
∴PA=PC,
∴△PAC为等边三角形,
∴∠P=60°.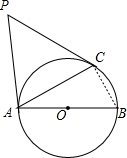
(Ⅱ)如图,连接BC,则∠ACB=90°.
在Rt△ACB中,AB=2,∠BAC=30°,
∵cos∠BAC=
,
∴AC=AB•cos∠BAC=2cos30°=
.
∵△PAC为等边三角形,
∴PA=AC,
∴PA=
.
∴PA⊥AB,
∴∠BAP=90°;
∵∠BAC=30°,
∴∠CAP=90°-∠BAC=60°.
又∵PA、PC切⊙O于点A、C,
∴PA=PC,
∴△PAC为等边三角形,
∴∠P=60°.

(Ⅱ)如图,连接BC,则∠ACB=90°.
在Rt△ACB中,AB=2,∠BAC=30°,
∵cos∠BAC=
| AC |
| AB |
∴AC=AB•cos∠BAC=2cos30°=
| 3 |
∵△PAC为等边三角形,
∴PA=AC,
∴PA=
| 3 |
点评:本题考查的是切线长定理,切线长定理图提供了很多等线段,分析图形时关键是要仔细探索,找出图形的各对相等切线长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 22、如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是( )
22、如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是( ) 如图,已知AB为半⊙O的直径,直线MN与⊙O相切于C点,AE⊥MN于E,BF⊥MN于F.
如图,已知AB为半⊙O的直径,直线MN与⊙O相切于C点,AE⊥MN于E,BF⊥MN于F. 如图,已知AB为⊙O的直径,直线l与⊙O相切于点D,AC⊥l于C,AC交⊙O于点E,DF⊥AB于F.
如图,已知AB为⊙O的直径,直线l与⊙O相切于点D,AC⊥l于C,AC交⊙O于点E,DF⊥AB于F. (2012•包头)如图,已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接BC,CF,AC.
(2012•包头)如图,已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接BC,CF,AC. (2012•呼和浩特)如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与弧AC相交于点E,连接BC.
(2012•呼和浩特)如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与弧AC相交于点E,连接BC.