Question

如图所示，△ABC，AB=AC，二次函数y=-

1

2

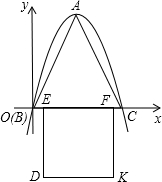x2+4x的图象经过点A、B、C，点E（1，0），F（7，0），将正方形EFKD沿y轴正方向进行移动，速度为每秒移动2个单位，移动时间为t（0＜t≤4），设移动过程中正方形与三角形部分重叠的面积为S
（1）求△ABC的面积S_△ABC；
（2）求重叠部分面积S关于时间t的函数关系式，并指出自变量t的取值范围；
（3）当正方形的点E、F移动到二次函数图象上，求重叠部分面积S，并请判断点D、K是否在△ABC外接圆上并说明理由；如不在，也请说明理由．

Answer 1

分析：（1）先求出B，C两点的坐标，从而求出线段BC的长，再求出顶点A的纵坐标即BC边上的高线，进而求△ABC的面积；
（2）分三种情况对问题进行讨论：①正方形EFKD的点E移动到直线AB的过程，正方形与三角形的重叠部分为矩形；②正方形EFKD继续向上移动，点D移动到x轴上的过程，正方形与三角形的重叠部分（1＜t≤3）；③正方形EFKD继续向上移动，点D移动到直线AB上的过程，正方形与三角形的重叠部如图3所示，分别求重叠部分面积S关于时间t的函数关系式即可．
（3）当正方形的点E、F移动到二次函数图象上，可求出此时的时间t，再把t代入二次函数的解析式进行验证即可的问题答案．

解答：解：（1）y=-

1

2

x2+4x=-

1

2

(x-4)2+8，
∴顶点A（4，8），
∵y=0时，-

1

2

x2+4x=0，
解得x₁=0，x₂=8
∴点B（0，0），点C（8，0），
所以S_△ABC=

BC•8

2

=

8×8

2

=32．

（2）分三种情况：
①正方形EFKD的点E移动到直线AB的过程，正方形与三角形的重叠部分为矩形，
如图1所示（0＜t≤1）S=2t•EF=12t，
②正方形EFKD继续向上移动，点D移动到x轴上的过程，正方形与三角形的重叠部分如图2所示（1＜t≤3），
易知：KW=2，BW=1，EK=2t-2△BKW∽△EHK，得EH=t-1（6分）S=12t-2（t-1）²=-2t²+16t-2，
③正方形EFKD继续向上移动，点D移动到直线AB上的过程，正方形与三角形的重叠部如图3所示（3＜t≤4），
由②得EH=t-1S=36-2（t-1）²=-2t²+4t+34，
重叠部分面积S关于时间t的函数关系式S=

12t(0＜t≤1) -2t2+16t-2(1＜t≤3) -2t2+4t+34(3＜t≤4)

，
（3）不存在
∵当正方形的点E、F移动到二次函数图象上，t=1.75，
∴S=-2×1.752+16×1.75-2=

159

8

，
此时点D、K不在△ABC外接圆上，
易求出△ABC的外接圆的半径为5，
设△ABC的外接圆的圆心为O，OD=

42+(3+2.5)2

≠5，
所以点D不在△ABC外接圆上，同理点K也不在△ABC外接圆上．

点评：本题考查了二次函数和几何图形（等边三角形，正方形）的综合应用，这类试题一般难度较大．解这类问题关键是善于将函数问题转化为方程问题，善于利用几何图形的有关性质、定理和二次函数的知识，并注意挖掘题目中的一些隐含条件．