题目内容
1.△ABC中已知AB=13,BC=10,D是BC中点,AD=12,求AC.分析 先由线段中点的定义得出BD=CD=$\frac{1}{2}$BC=5,再根据勾股定理的逆定理得到AD⊥BC,又D是BC中点,那么AD是BC的垂直平分线,根据线段垂直平分线的性质得出AC=AB=13.
解答 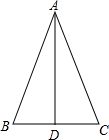 解:如图.
解:如图.
∵D是BC中点,
∴BD=CD=$\frac{1}{2}$BC=5.
∵△ABD中,AB=13,AD=12,BD=5,52+122=132,
∴△ABD是直角三角形,即AD⊥BC,
∵点D为BC边上的中点,
∴AD是BC的垂直平分线,
∴AC=AB=13.
点评 本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.也考查了线段中点的定义以及线段垂直平分线的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.二次函数y=2x2-4x-1的顶点式是( )
| A. | y=(2x-1)2-2 | B. | y=2(x-1)2-3 | C. | y=2(x+1)2-3 | D. | y=2(x+1)2+3 |
6.已知:⊙O的直径等于4,点P到圆心O的长度OP=4,则点P与⊙O的位置关系为( )
| A. | P在⊙O上 | B. | P在⊙O内 | C. | P在⊙O外 | D. | 不确定 |
 如图,在△ABC中,AB=AD=DC,∠BAD=40°,则∠DAC=35°.
如图,在△ABC中,AB=AD=DC,∠BAD=40°,则∠DAC=35°.