题目内容
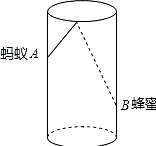
如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有乙滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外币A处到达内壁B处的最短距离为 .
练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
题目内容
如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有乙滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外币A处到达内壁B处的最短距离为 .

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案