Question

12．在⊙O中，AB、CD为两条弦，AB=CD，AB、CD交于点E，连结BD．
（1）如图1，求证：∠B=∠D：
（2）如图2，连结D并延长交弦AB于点F，连结AO交弦CD于点G，已知AB⊥CD．
①求证：CG=BF；
②当CE=$\frac{2}{5}$DG时，若BF=3，求⊙O的半径．

Answer 1

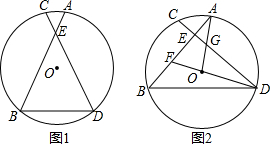
分析 （1）如图1，利用弦、弧的关系得到$\widehat{AB}$=$\widehat{CD}$，则$\widehat{AD}$=$\widehat{BC}$，然后根据圆周角定理可得∠B=∠D；
（2）如图2，先由（1）得∠B=∠EDB=45°，再利用圆周角定理得到∠AOD=2∠B=90°，然后证明△AOF≌△DOG得到GD=AF，于是有CG=BF；
②设CE=2x，DG=5x，则AF=DG=5x，接着表示出AE=CE=2x，EG=3-2x，DE=3+3x，EF=3x，然后通过证明△AEG∽△DEF，则利用相似比可求出x=1，从而得到EG=1，AE=2，DG=5，再利用勾股定理计算出AG=$\sqrt{5}$，最后证明△AEG∽△DOG，则利用相似比可计算出OD．

解答 （1）证明：如图1，
∵AB=CD，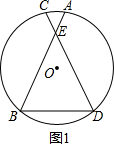
∴$\widehat{AB}$=$\widehat{CD}$，
∴$\widehat{AB}$-$\widehat{AC}$=$\widehat{CD}$-$\widehat{AC}$，
即$\widehat{AD}$=$\widehat{BC}$，
∴∠B=∠D；
（2）①证明：如图2，
∵AB⊥CD，
∴∠BED=90°，
由（1）得∠B=∠EDB，
∴∠B=45°，
∴∠AOD=2∠B=90°，
∴∠AOF=∠BOG=90°，
∵∠1+∠3=∠2+∠3=90°，
∴∠1=∠2，
在△AOF和△DOG中
$\left\{\begin{array}{l}{∠1=∠2}\\{∠AOF=∠DOG}\\{OA=OD}\end{array}\right.$，
∴△AOF≌△DOG，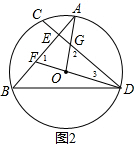
∴GD=AF，
∵AB=CD，
∴CG=BF；
②设CE=2x，DG=5x，则AF=DG=5x，
∵∠B=∠EDB，
∴EB=ED，
∵AB=CD，
∴AE=CE=2x，
由①得CG=BF=3，
∴EG=3-2x，
DE=DG+EG=5x+3-2x=3+3x，
EF=AF-AE=5x-2x=3x，
∵∠1=∠2=∠AGE，∠AEG=∠DEF=90°，
∴△AEG∽△DEF，
∴AE：DE=EG：EF，即2x：（3+3x）=（3-2x）：3x，解得x₁=1，x₂=-$\frac{3}{4}$（舍去），
∴EG=1，AE=2，DG=5，
在Rt△AEG中，AG=$\sqrt{A{E}^{2}+E{G}^{2}}$=$\sqrt{5}$，
∵∠2=∠AGE，∠AEG=∠DCG，
∴△AEG∽△DOG，
∴AE：OD=AG：DG，即2：OD=$\sqrt{5}$：5，解得OD=2$\sqrt{5}$，
∴⊙O的半径是2$\sqrt{5}$．

点评 本题考查了圆的综合题：熟练掌握圆周角定理和圆心角、弧、弦之间的关系；会运用三角形全等的知识解决线段相等的问题，运用勾股定理和相似比计算线段的长．解决（2）小题的第2个问题，通过代数法表示线段的长，再利用相似比建立方程可求出相应线段的长．