题目内容
4.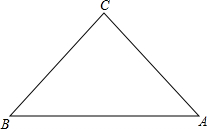 已知:如图,在△ABC中,AC=BC=5,AB=6,请以点A为原点,以AB所在的直线为x轴建立平面直角坐标系,并求出△ABC的各顶点坐标.
已知:如图,在△ABC中,AC=BC=5,AB=6,请以点A为原点,以AB所在的直线为x轴建立平面直角坐标系,并求出△ABC的各顶点坐标.
分析 以点A为原点,以AB所在的直线为x轴建立平面直角坐标系,然后过点C作AD⊥AB于D,根据等腰三角形三线合一的性质可得BD=AD=$\frac{1}{2}$AB,再利用勾股定理列式求出CD,然后写出各点的坐标即可
解答 解:坐标系如图,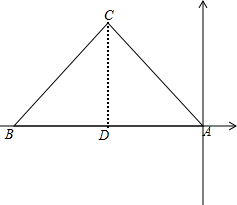
过点C作CD⊥AB于D,
∵AB=AC=13,BC=10,
∴BD=AD=$\frac{1}{2}$AB=$\frac{1}{2}$×6=3,
由勾股定理得,CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4.
∴A(0,0),B(-6,0),C(-3,4).
点评 此题考查坐标与图形的性质,等腰三角形三线合一的性质,勾股定理的应用,作底边上的高,构造出直角三角形并利用性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.某项科学研究,以45分钟为一个时间单位,并以每天上午10时为基准0,10时以前记为负,10时以后记为正,例如9:15记为-1,10:45记为1,依此类推,上午7:45应记为( )
| A. | 3 | B. | -3 | C. | -2.5 | D. | -7.5 |
16.关于x的一元二次方程x2$-\sqrt{2}x+\frac{1}{2}=0$的根的情况是( )
| A. | 有两个相等的实数根 | B. | 可能有实数根,也可能没有 | ||
| C. | 有两个不相等的实数根 | D. | 没有实数根 |
14.点A的坐标为(-2,3),点B与点A关于原点对称,则点B的坐标为( )
| A. | (-3,2) | B. | (-2,-3) | C. | (3,-2) | D. | (2,-3) |
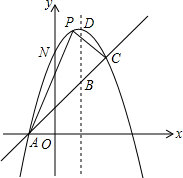 如图,已知抛物线y=-x2+bx+c过(1,4)与(4,-5)两点,且与一直线y=x+1相交于A,C两点,
如图,已知抛物线y=-x2+bx+c过(1,4)与(4,-5)两点,且与一直线y=x+1相交于A,C两点,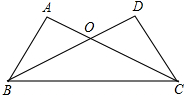 如图,∠A=∠D,OA=OD,∠DOC=50°,则∠DBC=25度.
如图,∠A=∠D,OA=OD,∠DOC=50°,则∠DBC=25度.