题目内容
如图,在△ABC中,已知AB=AC,∠BAC=90°,BC=6cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒2厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒1厘米的速度运动,连接AD、AE,设运动时间为t秒.
(1)求AB的长;
(2)当t为多少时,△ABD的面积为6cm2?
(3)当t为多少时,△ABD≌△ACE,并简要说明理由.(可在备用图中画出具体图形)



y=﹣ x+3
x+3

(3)动点E从点C沿射线CM方向运动2秒或当动点E从点C沿射线CM的反向延长线方向运动6秒时,△ABD≌△ACE.
理由如下:(说理过程简要说明即可)
①当E在射线CM上时,D必在CB上,则需BD=CE.
∵CE=t,BD=6﹣2t∴t=6﹣2t∴t=2
证明:∵AB=AC,∠B=∠ACE=45°,BD=CE,
∴△ABD≌△ACE.
②当E在CM的反向延长线上时,D必在CB延长线上则需BD=CE.
∵CE=t,BD=2t﹣6∴t=2t﹣6∴t=6
证明:∵AB=AC,∠ABD=∠ACE=135°,B D=CE
D=CE
∴△ABD≌△ACE.

练习册系列答案
相关题目
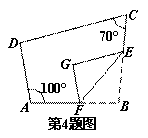
 的菱形OABC的顶点A,C,
的菱形OABC的顶点A,C, B分别在OD,OE,
B分别在OD,OE, 上,若把扇形DOE围成一个圆锥,则此圆锥的高为( )
上,若把扇形DOE围成一个圆锥,则此圆锥的高为( )  B.
B. C
C D.
D.

 0.60)
0.60)


 的结果______________________.
的结果______________________.