题目内容
下面是某同学在一次测验中解答的填空题:其中答案完全正确的题目个数为( )
(1)若x2=a2,则x=a;
(2)方程2x(x-1)=x-1的解为x=0;
(3)若直角三角形有两边长分别为3和4,则第三边的长为5.
(1)若x2=a2,则x=a;
(2)方程2x(x-1)=x-1的解为x=0;
(3)若直角三角形有两边长分别为3和4,则第三边的长为5.
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:解一元二次方程-因式分解法,解一元二次方程-直接开平方法,勾股定理
专题:计算题
分析:利用直接开平方法解方程对(1)进行判断;
根据因式分解法解方程对(2)进行判断;
根据分类讨论和勾股定理对(3)进行判断.
根据因式分解法解方程对(2)进行判断;
根据分类讨论和勾股定理对(3)进行判断.
解答:解:若x2=a2,则x1=a,x2=-a,所以(1)错误;
2x(x-1)=x-1,
2x(x-1)-(x-1)=0,
(x-1)(2x-1)=0,
x-1=0或2x-1=0,
所以x1=1,x2=
,所以(2)错误;
若直角三角形有两边长分别为3和4,当3与4为直角边时,第三边的长为5;当4为斜边时,第三边的长=
=
,所以(3)错误.
故选A.
2x(x-1)=x-1,
2x(x-1)-(x-1)=0,
(x-1)(2x-1)=0,
x-1=0或2x-1=0,
所以x1=1,x2=
| 1 |
| 2 |
若直角三角形有两边长分别为3和4,当3与4为直角边时,第三边的长为5;当4为斜边时,第三边的长=
| 42-32 |
| 7 |
故选A.
点评:本题考查了解一元二次方程-因式分解法:先把方程右边变形为0,然后把方程左边进行因式分解,这样把一元二次方程转化为两个一元一次方程,再解一次方程可得到一元二次方程的解.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
已知点M(-9,1-a)在x轴上,则a=( )
| A、0 | B、1 | C、2 | D、3 |
若2a<3a,则a一定满足( )
| A、a>0 | B、a<0 |
| C、a≥0 | D、a≤0 |
下列说法不正确的是( )
| A、有理数和无理数统称为实数 |
| B、实数是由正实数和负实数组成 |
| C、实数都可以表示在数轴上 |
| D、实数和数轴上的点一一对应 |
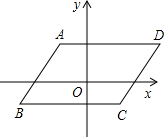 如图,平行四边形ABCD中,AD∥x轴,下列说法正确的是( )
如图,平行四边形ABCD中,AD∥x轴,下列说法正确的是( )| A、A与D的横坐标相同 |
| B、C与D的横坐标相同 |
| C、B与C的纵坐标相同 |
| D、B与D的纵坐标相同 |
比1小2的数是( )
| A、-1 | B、1 | C、3 | D、-2 |