Question

如图，AB是⊙O的直径，CB是弦，OD⊥CB于E，交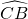于D，连接AC
①请写出两个不同类型的正确结论．
②若CB=16，ED=4，求⊙O的半径．

Answer 1

解：（1）不同类型的正确结论有：①BE=CE，②=，③∠BED=90°，④∠BOD=∠A，
⑤AC∥OD，⑥AC⊥BC，⑦OE²+BE²=OB²，⑧S_△ABC=AC•CE等．（写出2个即可），

（2）设⊙O的半径为x，则OE=x-4，
∵OD⊥BC，
∴CE=EB=BC=8；
在Rt△OBE中，
∵OE²+EB²=OB²，
∴（x-4）²+8²=x²，
解得x=10，
所以⊙O的半径是10．
分析：因为AB是⊙O的直径，可得∠ACB=90°，由OD⊥CB，可利用垂径定理得出一些结论如BE=CE、等．第二问直接利用垂径定理把问题放在Rt△OBE中解决．
点评：此题主要考查垂径定理、直径所对的圆周角是直角．由此知识还可以综合运用，得出旧知识．