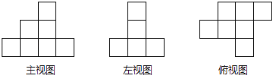
题目内容
【题目】如图,AB是⊙O的直径,过⊙O外一点P作⊙O的两条切线PC,PD,切点分别为C,D,连接OP,CD.
(1)求证:OP⊥CD;
(2)连接AD,BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的长.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)先判断出Rt△ODP≌Rt△OCP,得出∠DOP=∠COP,即可得出结论;
(2)先 求出∠COD=60°,得出△OCD是等边三角形,最后用锐角三角函数即可得出结论.
(1)证明:如图,连接OC,OD,则OC=OD.
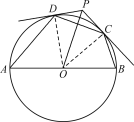
∵PD,PC是⊙O的切线,
∴∠ODP=∠OCP=90°.
在Rt△ODP和Rt△OCP中,
![]() ,
,
∴Rt△ODP≌Rt△OCP,
∴∠DOP=∠COP.
∵OD=OC,
∴OP⊥CD.
(2)连接AD,BC如图所示,则OA=OD=OC=OB=2,
∴∠ADO=∠DAO=50°,
∠BCO=∠CBO=70°,
∴∠AOD=80°,∠BOC=40°,
∴∠COD=60°.
∵OD=OC,
∴△COD是等边三角形.
由(1)知,∠DOP=∠COP=30°,
在Rt△ODP中,OP=![]() =
=![]() .
.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目