题目内容
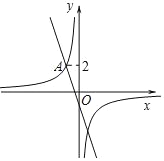
【题目】如图，在平面直角坐标系xOy中，直线y＝kx+m与双曲线y＝﹣
相交于点A（m，2）．
（1）求直线y＝kx+m的表达式；
（2）直线y＝kx+m与双曲线y＝﹣的另一个交点为B，点P为x轴上一点，若AB＝BP，直接写出P点坐标．
【答案】（1）m＝﹣1；y＝﹣3x﹣1；（2）P1（5，0），P2（
，0）．
【解析】
（1）将A代入反比例函数中求出m的值,即可求出直线解析式,
（2）联立方程组求出B的坐标,理由过两点之间距离公式求出AB的长,求出P点坐标,表示出BP长即可解题.
解：（1）∵点A（m，2）在双曲线
上，
∴m＝﹣1，
∴A（﹣1，2），直线y＝kx﹣1，
∵点A（﹣1，2）在直线y＝kx﹣1上，
∴y＝﹣3x﹣1．
（2）
，解得
或
，
∴B（
，﹣3），
∴AB＝
＝
，设P（n，0），
则有（n﹣）2+32＝
解得n＝5或
，
∴P1（5，0），P2（，0）．
练习册系列答案
阅读快车系列答案
相关题目
