题目内容
如图所示，在等腰梯形ABCD中，∠B=45°，已知腰长是3cm，则∠ADC=分析：根据等腰梯形的性质得到∠C=45°，∠ADC+∠C=180°，可以得到∠ADC的度数．在直角△CDE中，用正弦可以求出梯形的高．
解答：解：∵ABCD是等腰梯形，∴∠B=∠C=45°．
AD∥BC，∴∠ADC+∠C=180°，∴∠ADC=135°
在直角△CDE中，sinC=
即sin45°=
，∴DE=
．
故答案是：135°，
．
AD∥BC，∴∠ADC+∠C=180°，∴∠ADC=135°
在直角△CDE中，sinC=
| DE |
| DC |
| DE |
| 3 |
3
| ||
| 2 |
故答案是：135°，
3
| ||
| 2 |
点评：本题考查的是解直角三角形，根据等腰梯形的性质可以求出∠ADC的度数，然后根据正弦的定义求出梯形的高．
练习册系列答案
相关题目
25、如图所示，在等腰梯形ABCD中，AD∥BC，AB=CD，点P为BC边上任意一点，且
1、如图所示，在等腰梯形ABCD中，AD∥BC，DE⊥BC于点E，BF⊥AE于点F，请你添加一个条件，使△ABF≌△CDE．
48、如图所示，在等腰梯形ABCD中，AD∥BC，AB=CD，DE⊥BC于E，BF⊥AE于F，AE=BE．请你判断线段BF与图形中哪条线段相等，先写出你的猜想，再加以证明．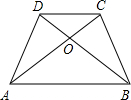
如图所示，在等腰梯形ABCD中，AB∥CD，若AB+CD=4，并且∠AOB=120°，则该等腰梯形的面积为
如图所示，在等腰梯形ABCD中，AD∥BC，过A作腰CD的平行线，AE∥CD，AB=AD=DC，∠B=60°