题目内容
修建某一建筑时,若请甲、乙两个工程队同时施工,8天可以完成,需付两队费用共3520元;若先请甲队单独做6天,再请乙队单独做12天可以完成,需付两队费用共3480元,问:
(1)甲、乙两队每天费用各为多少?
(2)若单独请某队完成工程,则单独请哪队施工费用较少?
(1)甲、乙两队每天费用各为多少?
(2)若单独请某队完成工程,则单独请哪队施工费用较少?
考点:二元一次方程组的应用
专题:
分析:(1)设甲每天费用为x元,乙每天费用为y元,根据题意可得等量关系:①甲、乙两个工程队同时施工,8天可以完成,需付两队费用共3520元;②甲队单独做6天,再请乙队单独做12天可以完成,需付两队费用共3480元,根据费用列出方程组,解方程组即可;
(2)设甲每天完成x,乙每天完成y,根据题意可得等量关系:①甲和乙8天的工作量=1,②甲6天的工作量+乙12天的工作量=1,根据等量关系列出方程组,再解可得甲和乙的工作效率,再求费用即可.
(2)设甲每天完成x,乙每天完成y,根据题意可得等量关系:①甲和乙8天的工作量=1,②甲6天的工作量+乙12天的工作量=1,根据等量关系列出方程组,再解可得甲和乙的工作效率,再求费用即可.
解答:
解:(1)设甲每天费用为x元,乙每天费用为y元,由题意得:
,
解得
.
答:甲每天的费用为300元,乙每天的费用为140元.
(2)设甲每天完成x,乙每天完成y,由题意得:
,
解得
,
甲单独做需要12天完成,乙单独做需要24天完成.
甲单独做需要12×300=3600元,乙单独做需要24×140=3360元.
答:乙队单独完成费用较少.
|
解得
|
答:甲每天的费用为300元,乙每天的费用为140元.
(2)设甲每天完成x,乙每天完成y,由题意得:
|
解得
|
甲单独做需要12天完成,乙单独做需要24天完成.
甲单独做需要12×300=3600元,乙单独做需要24×140=3360元.
答:乙队单独完成费用较少.
点评:此题主要考查了二元一次方程组的应用,关键是正确理解题意,找出题目中的等量关系,列出方程组.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
| 16 |
| A、4 | B、-4 | C、±2 | D、2 |
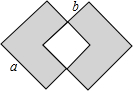 如图是两个大小相同的正方形,他们重合的部分(空白的部分)是一个小正方形,则阴影部分的面积为( )
如图是两个大小相同的正方形,他们重合的部分(空白的部分)是一个小正方形,则阴影部分的面积为( )| A、2a2-(a-b)2 |
| B、2a2-2(a-b)2 |
| C、(a-b)2 |
| D、2a2-b2 |
-2015的相反数是( )
| A、2015 | ||
| B、-2015 | ||
C、
| ||
D、-
|
 如图,∠AOB=60°,点P在∠AOB的角平分线上,OP=10cm,点E、F是∠AOB两边OA、OB上的动点,当△PEF的周长最小时,点P到EF距离是
如图,∠AOB=60°,点P在∠AOB的角平分线上,OP=10cm,点E、F是∠AOB两边OA、OB上的动点,当△PEF的周长最小时,点P到EF距离是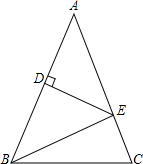 如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,垂足为D,∠EBC:∠EBA=1:2,求∠A的度数.
如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,垂足为D,∠EBC:∠EBA=1:2,求∠A的度数.